Урок № 38
Тема. Метричні співвідношення в колі
Мета: домогтися засвоєння учнями змісту теорем про пропорційність відрізків хорд, пропорційність відрізків січної і дотичної та змісту наслідків (про відрізки січних, проведених з однієї точки кола) та їх доведення.
Сформувати в учнів уміння:
– відтворювати зміст вивчених теорем;
– за готовими рисунками знаходити відрізки, про які йде мова в теоремах, та виконувати відповідні записи;
– застосовувати твердження теорем до розв’язування задач на обчислення
Закріпити знання учнями змісту ознаки подібності трикутників за двома кутами та властивості вимірювання вписаних кутів.
Тип уроку: засвоєння нових знань.
Наочність та обладнання: конспект “Застосування подібності трикутників”.
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
За необхідності перевірити виконання письмової частини домашнього завдання. Проводиться усна робота за готовими рисунками до домашніх задач.
Засвоєння змісту матеріалу попереднього уроку та формування оперативних умінь можна перевірити під час виконання
Самостійна робота
Варіант 1 | Варіант 2 |
1. У трикутнику зі сторонами 25 см і 40 см проведено бісектрису кута між даними сторонами. Вона ділить третю сторону на відрізки, менший з яких дорівнює 15 см. Знайдіть периметр трикутника | 1. У трикутнику ABC найбільша сторона АВ дорівнює 40 см. Бісектриса BD ділить сторону АС на відрізки завдовжки 15 см і 24 см. Знайдіть периметр трикутника ABC |
2. Бісектриса прямого кута прямокутного трикутника ділить гіпотенузу на відрізки завдовжки 15 см і 20 см. Знайдіть довжини відрізків гіпотенузи, на які її ділить висота трикутника | 2. Висота прямокутного трикутника ділить гіпотенузу на відрізки 12,6 см і 22,4 см. Знайдіть довжини відрізків гіпотенузи, на які її ділить бісектриса прямого кута |
III. Формулювання мети і завдань уроку
Учитель нагадує учням, що зміст теоретичного матеріалу, вивчення якого розпочалося на попередньому уроці, містить деякі співвідношення відрізків у трикутнику та в колі, які є результатом застосування до цих конфігурацій означення подібності трикутників (із попереднім доведенням подібності трикутників, утворених цими відрізками). Отже, мета уроку – вивчення інших, ніж на попередньому уроці, співвідношень.
IV. Актуалізація опорних знань
З метою свідомого засвоєння учнями змісту теорем та їх доведення учням слід активізувати знання і вміння щодо знання означень та властивостей хорд, дотичних та січних; означення вписаного кута та властивості вимірювання вписаного кута і наслідку з неї; ознак подібності трикутників.
Виконання усних вправ
1. Дайте назви всім відрізкам (рис. 1). Яка точка кола на рисунку 1 (б) найближча до точки А? Найвіддаленіша від точки А?
2. Чи все правильно на рис. 2?
3. ВС – дотична, О – центр кола, АВ = АС (рис. 3). Доведіть, що ОВ = ОС.
4. О – центр кола,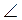 
АВС = 45° (рис. 4). Знайдіть кут АОС.
5. О – спільний центр кіл (рис. 5). Доведіть, що DA = ВС.
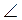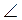6. MH – дотична, MAB = HAC (рис. 6). Доведіть, що АВ = АС.
V. Засвоєння знань
План вивчення нового матеріалу
1. Пропорційність відрізків хорд.
2. Пропорційність відрізків січної та дотичної.
3. Пропорційність відрізків січних.
@ На відміну від програми з геометрії попередніх років, за новою програмою з геометрії, метричні співвідношення в колі не є обов’язковими для вивчення у 8 класі. Проте, як і автори підручника, автор вважає, що вивчення питання про застосування подібності без вивчення цих теорем було б неповним. Тому, залежно від рівня підготовки учнів, вивчення нового матеріалу можна провести відповідно до підручника (з формулюванням, доведенням та відпрацюванням умінь застосовувати викладені теореми) або, на розсуд учителя, ознайомити учнів лише зі змістом поданих тверджень як із додатковим матеріалом, застосування якого слід опрацювати на найпростіших задачах.
VI. Формування первинних умінь
Виконання усних вправ
1. Знайдіть (рис. 7):
1) АН і ВС, якщо DM = 4, НВ = 5, НС = 10, AD = 3;
2) AC, AD : ВС, якщо АН : НС = 3 : 2, DH = 4, НВ = 6.
2. Знайдіть (рис. 8):
1) АР, якщо АР = DP, AC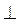
BP, АС = 12, СК = 4, ВК= 6;
2) радіус кола, якщо AD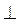ВК, АР = DP, BP = 4PM, DC = 2, СК = 1, ВС = 20.
3. МС – дотична, МС = 6, АС = СВ, СК = 3, АВ = 12 (рис. 9). Знайдіть 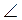ABC.
Виконання письмових вправ
1. При перетині з діаметром кола, хорда ділиться на відрізки завдовжки 3 см і 4 см, а діаметр – у відношенні 1 : 3. Знайдіть радіус кола.
2. Із точки поза колом, віддаленої від найближчої точки кола на 24 см, проведено дотичну до кола. Знайдіть радіус кола, якщо відрізок дотичної дорівнює 36 см.
3. Хорда перпендикулярна до діаметра. Відстані від одного з кінців хорди до кінців діаметрів дорівнюють відповідно 10 см і 24 см. Обчисліть довжини хорди і діаметра.
4. Із точки поза колом проведено дотичну, довжина якої дорівнює 12 см. Обчисліть радіус кола, якщо відстань від цієї точки до кола дорівнює 9 см.
@ Виконання учнями усних вправ сприяє закріпленню знань вивчених метричних співвідношень та формуванню первинних умінь їх застосування. Письмові вправи спрямовані на формування в учнів умінь виконувати рисунки за описом ситуації з використанням знань термінології, відповідних до ситуації співвідношень, а також виконання обчислень.
VI. Підсумки уроку
До кожного з наведених рисунків виберіть відповідну рівність. Поясніть свій вибір.
1) АЕ – BE = СЕ – DE;
2) АС – ВС = CD – СЕ;
3) AC – BC = CD2.
VIII. Домашнє завдання
Вивчити зміст метричних співвідношень у колі.
Розв’язати задачі
1. Січна, проведена з точки А, перетинає коло в точках В і С, причому АВ = 4 см, ВС = 5 см. Знайдіть довжину відрізка дотичної, проведеної до кола з точки А.
2. Катет прямокутного трикутника дорівнює 18 см. Точка на цьому катеті віддалена від гіпотенузи й іншого катета на 8 см. Знайдіть периметр трикутника.
Повторити властивість бісектриси трикутника; теорему Піфагора та наслідки з неї.
Задача (на повторення). При перетині двох хорд одна з них ділиться на відрізки 6 см і 16 см, а друга – у відношенні 3 : 2. Знайдіть довжину другої хорди.
(1 votes, average: 5,00 out of 5)