Урок № 8 2
Тема. Множення двох раціональних чисел з різними знаками
Мета: сформувати уявлення про зміст дії множення двох раціональних чисел з різними знаками та виробити вміння використовувати цей алгоритм для обчислення значень виразів.
Тип уроку: застосування знань, умінь і навичок.
Хід уроку
І. Перевірка домашнього завдання
1) Математичний диктант
Варіант 1 [2]
1. Запишіть у вигляді виразу добуток -3 та -4 [-5 та -7].
2. Виконайте множення:
А) -5 на -8 [-7 на-9];
Б) – на -4 [-15 на –
на -4 [-15 на –
В) -5,3 на -0,1 [-0,01 на -23].
3. Порівняйте добутки: -2,3 і -7,3 та 2 і 7
і 7 [-3
[-3 і –
і – та 3,15 і +2,1].
та 3,15 і +2,1].
@ Під час перевірки результатів виконання математичного диктанту повторюємо правило множення двох чисел з однаковими знаками.
II. Актуалізація опорних знань
Усні вправи
1. Прочитайте вирази: а) 11-12; б) 11-12 + 5; в) 11-(12 + 5); г) 11-(12 – 5).
2. Обчисліть: а) 10 – 15; б) 11 – 12; в) 24 – 5; г) 24 – 25; д) 25 – 16 (використовуючи прийоми швидкої лічби).
3. Замість * поставте знак “>” або “<“,
III. Формування знань
Задача 1. Температура повітря знижується щогодини на 2 °С. Зараз термометр показує 0 °С. Яку температуру повітря буде показувати термометр через 3 год?
Розв’язання. Оскільки зараз температура 0 °С, і щогодини вона знижується на 2 °С, то через три години вона буде -2 + (-2) + (-2) = -6 градусів. Цей самий результат можна було дістати, позначивши погодинне зниження температури як -2 °С, а наступний час + 3 год й виконати дію: (-2) – (+3) = -6.
Отже, (-2) • (+3) = -6. (1)
Задача 2. Зараз температура повітря 0 °С і щогодини вона підвищується на 2 °С. Яку температуру показував термометр 3 год тому?
Розв’язання. Оскільки зараз 0 °С, і щогодини температура підвищувалась на 2 °С, то зрозуміло, що три години тому вона була -6 °С. Цей же самий результат можемо дістати, позначивши щогодинну зміну температури як+2 °С, а час, що пройшов, -3 год (ми “повертаємось” у часі назад). Тоді маємо: +2 – (-3) = -6. (2)
Можна розглянути кілька наочних прикладів, записати рівності, подібні до (1) та (2), і порівняти їх, діставши такий висновок: Щоб помножити два числа з однаковими знаками, треба:
1) перемножити їх модулі;
2) перед результатом поставити знак “-“, тобто:
Добуток двох чисел з різними знаками є число від’ємне; модуль цього числа дорівнює добутку модулів даних чисел.
Наприклад
А) -8 – (+5) = -(|-8| – |+5|) = – (8 – 5) = -40,
Можна писати коротко (модулі обчислювати усно): -8 – (+5) = – (8 – 5) = -40;
Б) +1,7 – (-5) = – (1,7 – 5) = -8,5.
Зауваження. Під час множення як і під час додавання раціональних чисел спочатку можна визначати знак результату, а потім вже виконувати дію з модулями.
IV. Закріплення знань. Вироблення вмінь
Усні вправи
1. Прочитайте рівності. Чи є вони правильними?
А) -3 – (-2) = -6; б) -3 – (+2) = +6; в) +3 – (-2) = -6; г) -(+3) – (-2) = 6.
2. Який знак має добуток?
А) -3 – (-1,5); б) 9 – (107); в) – – 0,5; г) а – b, якщо а > 0, b < 0?
– 0,5; г) а – b, якщо а > 0, b < 0?
3. Обчисліть: а) -4 – (-10); б) -7 – (+6); в) +8 – (+0,02); г)  ; д)
; д)  ; є) -0,01-(-0,1); ж) -0,1-(+9).
; є) -0,01-(-0,1); ж) -0,1-(+9).
Письмові вправи
@ На цьому уроці ми вже виконуємо вправи на множення як чисел з однаковими знаками, так і чисел з різними знаками. Але, як і на попередньому уроці, кожного разу вимагаємо відтворення відповідного алгоритму.
1. Виконайте множення: а) 11-72; б) -11 – (-72); в) -11 – 72; г) 11 – (-72). Звернути увагу на те, що, обчисливши добуток модулів (у п. а), у наступних прикладах ми повинні тільки визначити знак добутку і поставити його перед добутком модулів (повторюємо алгоритм усного множення двоцифрового числа 1).
2. Виконайте множення:
А) -16 – 2,5; б) 0,01 – (- 65); в) -100 – 0,02; г) -4 – (-10,5); д) -5 – 3 ; є)
; є)  –
– ; ж) -3
; ж) -3 –
– ; з) 5,6 –
; з) 5,6 –  .
.
Перед виконанням дій вимагати від учнів аналізу того, із яким саме випадком множення маємо справу.
3. Обчисліть: а) -16 + 8 – (-0,5); б) -2 – (-1,8 – 1,2); в) -8 – 0,5 + 5 – (-0,6); г) 5 –
– + 6; д) –
+ 6; д) – +
+ –
– ; е)
; е)  –
– –
– –
– .
.
Перед виконанням дій вимагати:
А) визначити правильний порядок виконання дій;
Б) повторити алгоритми множення та додавання раціональних чисел.
4. Поставте замість зірочки знак “<” або “>” так, щоб утворилась правильна нерівність: а) 100 – (- 3) * 300; б) 0,2 – (-14) * -2,5.
Додаткові вправи
5. Обчисліть:
А) (- 7,6 – 5,8 + 4,5) – (6,3 – 8,2);
Б) -2,69 – (-0,8) + 0,7 – (4,3 – 7,8);
В) -10,8 – (-7,6 – 6,8) – (-3,5);
Г) (- 7,65 – (- 0,4) – 5) – (3 – 1,02);
Д) (- 2,36 + 6,82 – 5,45) – (46,5 – 91,5) + (- 45,09).
6. Обчисліть: а) 5,6 –  – (-5) – 3
– (-5) – 3 ; б) -0,75 –
; б) -0,75 –  – 7
– 7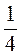 – (-0,3); в) (-3,4) –
– (-0,3); в) (-3,4) –  ; г)
; г)  .
.
Більш складні завдання на сумісні дії множення і додавання раціональних чисел.
7. Логічна вправа (на повторення)
Знайдіть і поставте замість (?) пропущений рисунок:




?
V. Підсумок уроку
1. Як виконати множення двох чисел, якщо вони: а) з однаковими знаками, б) з різними знаками?
2. Що більше добуток двох чисел з однаковими знаками чи добуток двох чисел з різними знаками?
3. Замість * поставте знаки “+” або “-“, щоб рівності стати правильними: а) *5 – *2 = -10; б) *5 – *2 = 10; в) (-5) – (-2) = *10.
VI. Домашнє завдання
Усні вправи
1. Обчисліть а) 8 – 6; б) 8 – (- 6); в) -8 – 6; г) -8 – (-6); д) 7 – (-4); є) (-7) – (-4); ж) -5 – 4; з) -100 – 0.
2. Обчисліть а) – 0,2 -3; б) 2 – (-0,6); в) (-1,2) – (-2), г) -0,1 – (-20).
Письмові вправи
1. Виконайте множення а) -12 – 25; б) 1,3 – (-5); в) -10 – (-70,1), г) -5,45 – (-1,02); д) 105 – (-0,18); є) 12 –  ; ж) –
; ж) – –
–  ; з) -4
; з) -4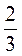 – 1
– 1 .
.
2. Обчисліть а) – 0,4 – (-10) – 7; б) – 0,3 – 1,2 – 2,5; в) (0,1 – 0,6) – 8; г) -0,7 – 6 + 7,2 – 0,2, д)  ; є)
; є)  .
.
3. Обчисліть 1,2 – (-6,39 + 4,84) –  – 24,6.
– 24,6.
Вправа на повторення
На першій книжковій полиці на 60 книжок більше, ніж на другій Скільки книжок на кожній полиці, якщо кількість книжок на другій полиці становить  кількості всіх книжок?
кількості всіх книжок?
