УРОК № 54
Тема. Пряма призма. Площа поверхні та об’єм призми
Мета уроку: повторити, привести в систему й розширити відомості про многогранники, пряму призму, площу поверхні та об’єм призми.
Тип уроку: комбінований.
Наочність і обладнання: таблиця “Початкові відомості стереометрії” [13], моделі прямих призм.
Вимоги до рівня підготовки учнів: пояснюють, що таке пряма призма та її елементи; зображують і знаходять на рисунку пряму призму; записують і пояснюють формули площі поверхні та об’єму прямої призми; застосовують
Хід уроку
І. Перевірка домашнього завдання
1. Перевірити правильність виконання домашнього завдання за записами, зробленими на дошці до початку уроку.
Задача 1
Дано: ABCDA1B1C1D1 – прямокутний паралелепіпед (рис. 241, с. 228). АВ = ВС = 2 см, ВВ1 = 1 см.
Знайдіть: ВВ1, В1А1, В1С1, B1D1, B1С, B1D, B1A.
Розв’язання
ВВ1 = 1 см. А1В1 = В1С1 = 2 см,
B1D1 =  =
=  = 2
= 2 (см).
(см).
B1A = B1C =  =
=  (см).
(см).
B1D = 
 = 3 (см).
= 3 (см).
Задача 2. Нехай? || ?, a || b (рис. 242). Прямі a i b перетинають площини? і? у точках A1, А2 і В1, В2. Через прямі a і b проведемо площину?, яка перетинає? і? на прямих А1B1 і А2В2, причому А1В1 || А2В2.

Тоді А1А2В2В1 – паралелограм, оскільки в нього протилежні сторони попарно паралельні, а в паралелограмі протилежні сторони рівні. Отже, А1А2 = В1В2.
2. Фронтальна бесіда 1) Яким може бути взаємне розміщення двох різних площин у просторі? 2) Які дві площини називаються паралельними? 3) Наведіть приклади паралельних площин у предметів із оточуючого середовища. 4) У якому випадку дві площини будуть паралельними? 5) Як можуть розташовуватися в просторі пряма і площина? 6) Сформулюйте означення прямої, перпендикулярної до площини. 7) Що таке перпендикуляр? похила?
II. Самостійна робота
Самостійну роботу навчального характеру можна провести за посібником [14], тест 17 “Прямі і площини в просторі”.
III. Поетапне сприймання й усвідомлення нового матеріалу
Многогранник та його елементи
Фігури, які вивчає стереометрія, називають тілами. Наочно тіло уявляють як частину простору, зайняту фізичним тілом і обмежену поверхнею. (Демонструємо моделі многогранників.)
Многогранником називається тіло (частина простору), обмежене скінченною кількістю плоских многокутників (рис. 243). Многокутники, які обмежують многогранник, називають його гранями, їх сторони – ребрами, а вершини – вершинами многогранника.
На рис. 243 гранями є многокутники: ABC, А1В1С1, АВВ1A1, ВВ1C1С, АА1C1С; ребрами – сторони АС, ВС, АВ, АА1, ВВ1, CC1, A1B1, A1C1, B1C1, вершинами – точки А, В, С, A1, В1, С1.

Завдання класу
1. Наведіть приклади предметів побуту, які мають форму многогранників. 2. Скільки вершин, ребер, граней має: а) паралелепіпед; б) куб? 3. Яке найменше число ребер може мати многогранник? 4. Побудуйте многогранник, який має 4 грані. Скільки ребер і скільки вершин він має? 5. Якщо поверхню многогранника розрізати по кількох його ребрах і розкласти на площині, то дістанемо розгортку даного многогранника. На рис. 244 наведено розгортки куба. Побудуйте розгортки куба, відмінні від наведених.

Призма та її елементи
Многогранник, дві грані якого – рівні n-кутники з відповідно паралельними сторонами, а всі інші п граней – паралелограми, називається n-кутною призмою (рис. 245). (Демонструємо моделі призм.)

Рівні n-кутники призми називаються основами, а паралелограми – бічними гранями, сторони основи – ребрами основи, інші ребра – бічними ребрами.
З означення призми випливає, що основи призми рівні, а також лежать у паралельних площинах. Бічні ребра паралельні й рівні.
Поверхня призми складається з основ і бічної поверхні. Площею поверхні призми називається сума площ усіх її граней. Оскільки основи рівні, то Snp = S6ічн + 2Sосн, де Snp – площа поверхні призми; S6ічн – площа бічної поверхні призми; Sосн – площа основи.
Завдання класу
1. Скільки граней має n-кутна призма? Чи може призма мати 10 граней? 2. Скільки ребер має п-кутна призма? Чи може призма мати 10 ребер? 3. Скільки вершин має п-кутна призма? Чи може призма мати 10 вершин? 4. Скільки граней має 15-кутна призма? А вершин? А ребер?
Призма називається прямою, якщо її бічні ребра перпендикулярні до основи. (Демонструються моделі прямих призм.)
Пряма призма називається правильною, якщо в її основі лежить правильний многокутник. (Демонструються моделі правильних призм.)
Слід зазначити, що бічними гранями прямої призми є прямокутники.
Площа поверхні та об’єм прямої призми
Теорема. Площа бічної поверхні прямої призми дорівнює добутку периметра її основи на довжину ребра.
Доведення
Нехай а1, а2, …, ап – сторони; основи призми, h – довжина бічного ребра (рис. 246).

Тоді а1 + а2 + … + аn = Р – периметр основи. Площа бічної поверхні дорівнює сумі площ усіх бічних граней:
Sбічн = a1h + a2h + … + anh = (а1 + а2 +… an)h = Ph.
Пряма призма, в основі якої лежить прямокутник, називається прямокутним паралелепіпедом. Прямокутний паралелепіпед, усі ребра якого рівні, називається кубом.
У молодших класах ви вже обчислювали об’єм прямокутного паралелепіпеда за формулою
V = abc, (1)
Де a, b, c – відповідно довжина, ширина і висота паралелепіпеда. Формулу (1) можна записати у вигляді
V = Sh, (2)
Де S = ab – площа основи, h = c – висота паралелепіпеда.
Формула (2) справедлива для будь-якої прямої призми. Отже:
Об’єм прямої призми дорівнює добутку площі її основи на довжину бічного ребра (висоту): V = Sh.
Завдання класу
1. Знайдіть площу поверхні куба, ребро якого дорівнює 5 см. 2. Знайдіть площу поверхні прямокутного паралелепіпеда, сторони основи якого дорівнюють 3 см і 4 см, а бічне ребро 5 см. 3. Основа прямої призми – прямокутний трикутник з катетами 3 см і 4 см, а бічне ребро дорівнює 5 см. Знайдіть площу повної поверхні призми. 4. Знайдіть об’єм куба, ребро якого дорівнює 5 см. 5. Знайдіть об’єм прямокутного паралелепіпеда, сторони основи якого дорівнюють 3 см і 4 см, а бічне ребро – 5 см. 6. Основа прямої призми – прямокутний трикутник з катетами 3 см і 4 см, а бічне ребро – 5 см. Знайдіть об’єм призми. Складаємо конспект учнів (табл. 10).
Таблиця 10
Призма
N-кутна призма – многогранник, дві грані якого – рівні n-кутники з відповідно паралельними сторонами, а всі інші грані – паралелограми.
ABCD, A1B1C1D1 – основи; АA1, ВВ1, СС1, DD1 – бічні ребра; АВ, ВС, CD, AD, А1В1, В1С1, С1D1, A1D1 – ребра основи.
Призма пряма – якщо бічні ребра перпендикулярні до основи.
Правильна призма – це пряма призма, в основі якої лежить правильний многокутник.

Sпр = Sбічн + 2Sосн.
Площа бічної поверхні прямої призми:
Sбічн = Р • h, P = a1 + a2 + …+ an.
Об’єм прямої призми: V = S • h
IV. Закріплення й осмислення нового матеріалу
Розв’язування задач
1. Знайдіть об’єм правильної трикутної призми, ребро основи якої дорівнює 2 см, а бічне ребро – 10 см. 2. Знайдіть площу бічної поверхні й площу повної поверхні трикутної призми, кожне ребро якої дорівнює 2 см. 3. В основі прямої призми лежить трикутник зі сторонами 7 см, 5 см, 6 см. Бічне ребро призми дорівнює 4 см. Знайдіть об’єм призми. 4. В основі прямої призми лежить ромб зі стороною 5 см і гострим кутом 30°. Висота призми дорівнює 6 см. Знайдіть об’єм призми, площу повної поверхні призми. 5. У прямокутному паралелепіпеді ABCDA1B1C1D1 ребра АВ = 3 см, AD = 4 см і АА1 = 5 см. Знайдіть площу поверхні та об’єм паралелепіпеда. (Відповідь. 94см2, 60см3.) 6. На рис. 247 зображено розгортку прямої трикутної призми. За наведеними даними знайдіть площу поверхні та об’єм призми. (Відповідь. 60см2, 24см3.)

7. Скирта сіна має форму прямої призми з п’ятикутною основою (рис. 248). Розміри скирти (у метрах) подано на рисунку. Знайдіть об’єм скирти та масу сіна в скирті, якщо густина сіна дорівнює 0,03 т/м3. (Відповідь. 19,8 т.)

8. Діагональ бічної грані правильної трикутної призми дорівнює l і утворює з бічним ребром кут?. Знайдіть площу бічної поверхні призми. (Відповідь. 312 sin? cos?.)
V. Самостійна робота
Варіант 1
1. Знайдіть площу бічної поверхні правильної трикутної призми, сторона основи якої дорівнює 3 см, а бічне ребро – 5 см. 2. Знайдіть об’єм прямої чотирикутної призми, в основі якої лежить ромб з діагоналями 12 см і 16 см, а бічне ребро – 10 см. 3. В основі прямої призми лежить квадрат. Діагональ призми дорівнює d і утворює з бічним ребром кут?. Знайдіть об’єм призми.
Варіант 2
1. Знайдіть об’єм правильної чотирикутної призми, сторона основи якої дорівнює 3 см, а бічне ребро – 5 см. 2. Знайдіть площу бічної поверхні прямої чотирикутної призми, в основі якої лежить ромб з діагоналями 12 см і 16 см, а бічне ребро дорівнює 10 см. 3. В основі прямої призми лежить прямокутний трикутник з гіпотенузою с і гострим кутом?. Бічне ребро призми дорівнює найбільшій стороні основи призми. Знайдіть об’єм призми.
Відповіді до завдань самостійної роботи
Варіант 1. 1. 45см2. 2. 960см3. 3.  D2 sin2? cos?.
D2 sin2? cos?.
Варіант 2. 1. 45 см3. 2. 400 см2. 3.  C3 sin? cos?.
C3 sin? cos?.
VI. Домашнє завдання
1. Вивчити формули площі поверхні та об’єму прямої призми. 2. Розв’язати задачі. 1) Знайдіть площу бічної поверхні й об’єм правильної шестикутної призми, якщо сторона її основи дорівнює 6 см, а висота – 5 см. 2) Знайдіть об’єм і площу повної поверхні прямої призми, в основі якої лежить прямокутний трикутник із катетами 3 см і 4 см, а бічне ребро призми дорівнює 10 см. 3) Знайдіть площу бічної поверхні правильної трикутної призми, площа основи якої дорівнює 4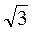 см2, а бічне ребро – 10 см.
см2, а бічне ребро – 10 см.
VII. Підбиття підсумків уроку
Запитання до класу
1. Що таке n-кутна призма? 2. Яка призма називається прямою? правильною? 3. Чому дорівнює площа бічної поверхні прямої призми? 4. Чому дорівнює об’єм призми? 5. Ребро куба дорівнює 5 см. Визначте, які з наведених тверджень є правильними, а які – неправильними.
А) Площа однієї грані куба дорівнює 20 см2.
Б) Площа поверхні куба дорівнює 150 см2.
В) Об’єм куба дорівнює 150 см3.
Г) Діагональ грані куба дорівнює 5 см.
см.
