Тематичне оцінювання № 6

Урок 61

Тема. Тематичне оцінювання № 6

Мета уроку: перевірка навчальних досягнень учнів з теми “Кути та вектори у просторі”.

Тематичне оцінювання № 6 можна провести шляхом виконання те­матичної контрольної роботи.

І. Тематична контрольна робота № 6

Варіант А

1. Сторона квадрата ОАВС дорівнює 5 (рис. 303). Запишіть координа­ти вектора . (3 бали)

2. Із точки, віддаленої від площини на відстані 10 см, проведено дві по­хилі, які утворюють з площиною кути в 45° і 30°.

Кут між їх проек­ціями дорівнює 90°. Знайти відстань між кінцями похилих. (3 бали)

3. Дано вектори (4; -2; -4) і (6; -3; 2). Обчисліть ( – )2 та кут між векторами і . (3 бали)

4. Ортогональною проекцією трапеції, площа якої дорівнює 80см2, є рівнобічна трапеція з основами 7 і 13 см і бічною стороною 5 см. Об­числіть кут між площиною трапеції і площиною її проекції. (3 бали).

1. Сторона квадрата ОАВС дорівнює 5 (рис. 304). Запишіть координа­ти вектора .

(3 бали)

2. Із точки, віддаленої від площини на відстані 10 см, проведено дві похилі, які утворюють з площиною кути в 30°, а між собою кут в 60°. Знайдіть відстань між кінцями похилих. (3 бали)

3. Дано вектори (4; -2; -4) і (6; -3; 2). Обчисліть ( + )2 та кут між векторами і . (3 бали)

4. Ортогональною проекцією трапеції є рівнобічна трапеція з основа­ми 7 і 25 см і діагоналями, які перпендикулярні до бічних сторін. Кут між площинами цих трапецій дорівнює 60°. Обчисліть площу даної трапеції. (3 бали).

1. Сторона квадрата ОАВС дорівнює 5 (рис. 305). Запишіть координа­ти вектора . (3 бали)

2. Із точки, що знаходиться на відстані 6 від площини, проведено до цієї площини дві похилі під кутом 30° до неї. Їх проекції утво­рюють 120°. Знайдіть відстань між кінцями похилих. (3 бали)

3. Дано: = 13, = 19, = 24 . Обчисліть . (3 бали)

4. Ортогональною проекцією даного трикутника, площа якого дорівнює 36См2, є прямокутний трикутник, катет якого дорівнює 12 см, а медіана, проведена до гіпотенузи, – 7,5 см. Обчисліть кут між площинами цих трикутників. Чи може даний трикутник бути пра­вильним? (3 бали).

1. Сторона квадрата ОАВС дорівнює 5 (рис. 306). Запишіть коор­динати вектора . (3 бали)

2. Із точки, віддаленої від площини на 8 см, проведено дві похилі під кутом 45° до площини. Знайдіть відстань між основами похилих, якщо кут між проекціями похилих дорівнює 120° . (3 бали)

3. Дано: = 11, = 23, = 30. Обчисліть . (3 бали)

4. Ортогональною проекцією даного трикутника є прямокутний три­кутник, гіпотенуза якого дорівнює 15 см, а катет – 9 см. Кут між площинами цих трикутників дорівнює 30°. Знайдіть площу даного трикутника. Чи може даний трикутник бути правильним? (3 бали).

Відповідь. Варіант 1. 1. (5; -5; 0) . 2. 20 см. 3. ( – )2 = 41, arccos . 4. 60°.

Варіант 2. 1. (5;0;-5). 2. 20см. 3. ( + )2 = 129, arccos. 4. 384см2.

Варіант 3. 1. (0;-5;5). 2. 18 см. 3. 22. 4. 30°, не може.

Варіант 4. 1. (5; 5; 0). 2. 8 см. 3. 20. 4. 36 см2, не може.

Варіант Б

Варіант 1

1. Дано точки А (1; 0; – 2), В (-2; 1; 3) і вектор (1; 0; – 2) . Знайдіть:

А) координати вектора ; (2 бали)

Б) абсолютну величину вектора ; (2 бали)

В) координати суми векторів і ; (2 бали).

2. Знайдіть довжину вектора 2+3, якщо (3; 1; 0), (0; 1; -1). (3 бали)

3. Знайдіть косинус кута С трикутника АВС, якщо А(0; 1; – 1), В (1; – 1; 2), С (3; 1; 0). (3 бали)

Варіант 2

1. Дано точки А(3; 2; 1), B(1; 2; 3) і вектор (1; 1; 1). Знайдіть:

А) координати вектора ; (2 бали)

Б) абсолютну величину вектора ; (2 бали)

В) координати різниці векторів і ; (2 бали).

2. Вектори і перпендикулярні, причому = 12, =16. Знай­діть . (3 бали)

3. Знайдіть косинус кута А трикутника АВС, якщо А(0; 1; -1), В (1; -1; 2), С (3; 1; 0). (3 бали)

Варіант 3

1. Дано вектор (1; 2; 3) та точки C (1; 0; 1) і D (1; 1; 2). Знайдіть:

А) координати вектора ; (2 бали)

Б) абсолютну величину вектора ; (2 бали)

В) координати вектора 3-. (2 бали).

2. Знайдіть довжину вектора 2 + 3, якщо (1; 1;-1), (2; 0; 0). (3 бали)

3. Знайдіть величину кута В трикутника АВС, якщо А (2; 2; -4), В(2; – 1; – 1), С(3; – 1; – 2). (3 бали)

Варіант 4

1. Дано вектор (1; – 1; 0) та точки C(1; 0; 2) і D(1; 1; 2). Знайдіть:

А) координати вектора ; (2 бали)

Б) абсолютну величину вектора ; (2 бали)

В) координати вектора 2-. (2 бали).

2. Вектори і перпендикулярні, причому = 6, = 8. Знай­діть . (3 бали)

3. Знайдіть величину кута А трикутника АВС, якщо А(2;-2;-3), В (4;- 2;- 1), С (2; 2; 1). (3 бали)

Тематичне оцінювання № 6 можна провести за допомогою тесту, текст якого подано нижче.

При оцінюванні виконання тестів враховуються тільки ті шість із виконаних завдань, яким відповідає найбільша кількість балів.

Мета даного тесту – перевірити, чи вміє учень:

– зображати точку, задану координатами, та виконувати обернену задачу;

– обчислювати відстань між двома точками, заданими координата­ми; знаходити координати середини відрізка;

– виконувати дії над векторами, заданими координатами;

– розв’язувати прості задачі на знаходження кута між прямою і площиною; між двома мимобіжними прямими; між площинами.

Варіант 1

1. Сторона квадрата ОАВС, який лежить у площині zу, дорівнює 1 (рис. 307). Знайдіть координати точки В. (1 бал)

2. а) В(1; 1; 0); б) В(0; 1; 1); в) В(1; 0; 1); г) В(1; 1; 1).

3. Дано точки A(2;3;1), B(1;0;2). Знайдіть координати вектора . (1 бал)

4. а) (3; 3; 3); б) (1; 3; -1); в) (-1; -3; 1); г) (-3; -3; -3).

5. Дано зображення куба (рис. 308). Знайдіть кут між прямими а і b. (1 бал)

6. а) 45°; б) 0°; в) 90°; г) визначити неможливо.

II рівень

1. Чому дорівнює відстань між точками А і В, якщо A(1;1;1), В(-1;-1;1)? (1 бал)

А) ; б) 2; в) 2; г) 8.

2. Яка з вказаних точок С є серединою відрізка АВ, якщо А(1; 2; 3), В(3; 1; 1)? (1 бал)

A) C(1; 1; 1); б) С(2; 2; 2); в) С(-1; 0; 2); г) С(4; 4; 4).

3. При яких значеннях п вектори (1; -1; n) і (n; 1; n) колінеарні? (1 бал)

А) Ні при яких; б) при n = -1; в) при n = 1; г) при n = ±1.

IІІ рівень

1. Знайдіть координати вершини D паралелограма ABCD, якщо А (0; 2; 0), В (1;0;0); С (2; 0; 2). (2 бали)

A) D(1;2;3); б) D(2;2;1); в) D(1;2;2); г) D(2;1;2).

2. З однієї точки до площини проведені рівні похилі. Кут між ними 60° , а між їх проекціями – 90° . Знайдіть кути між похилими і площиною. (2 бали)

А) 30°; б) 60°; в) 45°; г) 90°.

3. Дві площини перетинаються під кутом 60°. Точка М знаходиться від цих площин на відстані 4 см. Знайдіть відстань від точки М до лінії перетину площин. (2 бали)

А) 2 см; б) 4 см; в) 4 см; г) 8 см.

1. Дано точки А(2; 1; 7), В(-1; 1; 3), С(-8; 1; 2). Знайдіть внутріш­ній кут В трикутника АВС. (3 бали)

А) 45°; б) 60°; в) 135°; г) 90°.

2. Дано точки А(1; 0; 0), B(0; 0; 1), C(0; 1; 1), D(1; 1; 0). Знайдіть площу чотирикутника ABCD. (3 бали)

А) 1; б) ; в) 2; г) .

3. Знайдіть тангенс кута між діагоналлю куба і площиною однієї з його граней. (3 бали)

А) ; б) ; в) ; г) .

Варіант 2

1. Сторона квадрата ОАBС, який. лежить у площині ху, дорівнює 1 (рис. 309). Знайдіть координати точки В.

(1 бал) а) В(0; 1; 1); б) B(1; 0; 1); в) B(1; 1; 0); г) B(1; 1; 1).

2. Якому із вказаних векторів дорівнює вектор (1; 2; 3)? (1 бал)

А) (2; 3; 1); б) (3; 1; 2); в) (1; 2; 3); г) (1; 3; 2).

3. Дано зображення куба (рис. 310). Знайдіть кут між прямими а і b. (1 бал)

А) 45°; б) 0°; в) 90°; г) визначити неможливо.

1. Знайдіть довжину вектора , якщо А (-1; 1; -1), B(1; -1; -1). (1 бал)

А) ; б) 2; в) 2; г) 8.

2. Точка C(1; 1; 1) є серединою відрізка АВ, причому B(1; 3; -1). Знайдіть координати точки А. (1 бал)

А) А(0;0;0); б) А(1;0;3); в) А(1;-1;0); г) А(1;-1;3).

3. При якому значенні n вектори (2; 1; n) і (n; 1; n) перпендику­лярні? (1 бал)

А) n = 1; б) n = -1; в) n = ± 1; г) ні при яких n.

1. Знайдіть координати вершини А паралелограма ABCD, якщо B(1;0;1), C(1;1;0); D(1;1;1). (2 бали)

А) А(2; 1; 2); б) А ; в) А(1; 0; 2); г) А(2; 0; 1).

2. З однієї точки до площини проведені дві рівні похилі, які утворю­ють з перпендикуляром кути по 45°, а між собою – 60°. Знайдіть кут між проекціями похилих на цю площину. (2 бали)

А) 30°; б) 60°; в) 45°; г) 90°.

3. Дві площини перетинаються під кутом 60°. Точка М знаходиться на однаковій відстані від цих площин і на відстані 2 см до лінії перети­ну площин. Знайдіть відстань від точки М до цих площин. (2 бали)

А) 2 см; б) 1 см; в) 0,5 см; г) визначити неможливо.

IV рівень

1. Дано точки А(-1;-2;-1), В(-1;-1;0), С(-1; -1; -1). Знайдіть величину кута ВАС. (3 бали)

А) 135°; б) 60°; в) 90°; г) 45°.

2. Дано точки А(0; 2; 0), B(1; 0; 0), C(2; 0; 2), D (1; 2; 2). Знайдіть площу чотирикутника ABCD. (3 бали)

А) 2; б) 2; в) 2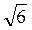; г) 2.

3. Дано тетраедр, усі ребра якого рівні. Знайдіть тангенс кута між біч­ним ребром і площиною основи тетраедра. (3 бали)

A) ; б) ; в) 1; г) визначити неможливо.

Відповіді до тестових завдань

Рівень	Номер завдання	Варіант 1	Варіант 2
І	1	Б	В
2	В	В
3	В	В
II	1	Б	В
2	Б	Г
3	А	Б
III	1	В	В
2	В	Г
3	Г	Б
IV	1	В	Г
2	Б	В
3	Г	Б

II. Домашнє завдання

Якщо в класі виконувалася тематична контрольна робота № 6, то вдома можна запропонувати виконати тест, і навпаки.

III. Підведення підсумку уроку

У ході фронтальної бесіди з’ясувати, які завдання викликали труд­нощі, та відповісти на запитання учнів.