Home ⇒ 📕Астрономія ⇒ Визначення відстаней до планет


Визначення відстаней до планет

§ 4. Закони руху планет

5. Визначення відстаней до планет

Для вимірювання відстаней до планет в астрономічних одиницях можна використати третій закон Кеплера, але для цього треба визначити геометричним методом відстань від Землі до будь-якої планети. Припустімо, що потрібно виміряти відстань L від центра Землі О до світила S. За базис приймають радіус Землі Rq і вимірюють кут <ASO = p, який називають горизонтальним паралаксом світила, бо одна сторона прямокутного трикутника – катет AS, є горизонтом для точки А (рис. 4.11). Горизонтальний паралакс

(від грец.- зміщення) світила – це кут, під яким було б видно перпендикулярний до променя зору радіус Землі, якби сам спостерігач перебував на цьому світилі. З прямокутного трикутника OAS визначаємо гіпотенузу OS:

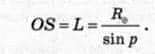Визначення відстаней до планет (4.4)

Визначення відстаней до планет

Рис. 4.11. Горизонтальний паралакс р світила визначає кут, під яким із цього світила було б видно перпендикулярний до променя зору радіус Землі

Горизонтальні паралакси деяких тіл

Місяць 10 = 60′

Венера 31″

Марс 23″

Сонце 8,8″

Нептун 0,2″

Правда, при визначенні паралаксу виникає проблема: як астрономи

можуть виміряти кут р з поверхні Землі, не літаючи в космос? Для того щоб визначити горизонтальний паралакс світила S, потрібно двом спостерігачам одночасно з точок А і В виміряти небесні координати (пряме сходження та схилення) цього світила (див. §2). Ці координати, які вимірюють одночасно з двох точок – А і В, трохи відрізнятимуться. На основі цієї різниці координат визначають величину горизонтального паралакса.

Чим далі від Землі спостерігається світило, тим менше буде значення паралакса. Наприклад, найбільший горизонтальний паралакс має Місяць, коли він перебуває найближче до Землі: р = 1°01′. Горизонтальний паралакс планет набагато менший, і він не залишається сталим, бо відстані між Землею та планетами змінюються. Серед планет найбільший паралакс має Венера – 31″, а найменший паралакс 0,21″ – Нептун. Для порівняння можна привести приклад, що під кутом 1″ видно літеру “О” у цій книзі з відстані 100 м – такі крихітні кути змушені вимірювати астрономи для визначення горизонтальних паралаксів тіл у Сонячній системі. Як виміряти відстань до зір, дивись у § 13.

Висновки

Усі космічні тіла від планет до галактик рухаються згідно із законом всесвітнього тяжіння, який був відкритий Ньютоном. Закони Кеплера визначають форму орбіти і швидкість руху планет Сонячної системи та їх періоди обертання навколо Сонця.


1 Star2 Stars3 Stars4 Stars5 Stars (1 votes, average: 5,00 out of 5)


Визначення відстаней до планет - Астрономія


Схожі записи:

  1. Планети-карлики §11. Малі тіла Сонячної системи 7. Планети-карлики Уперше цей новий клас тіл Сонячної системи визначили у серпні 2006 р. на з’їзді Міжнародного Астрономічного Союзу (МАС)...

  2. Меркурій § 8. Планети земної групи 2. Меркурій Меркурій є найменшою планетою Сонячної системи, яку рідко кому випадало спостерігати неозброєним оком, тому що вона розташована близько...

  3. Нептун §9. Планети-гіганти 5.Нептун Чи існує океан на планеті Нептун, яку назвали на честь бога підводного світу? Нептун розташовується на околиці Сонячної системи і має період...

  4. Приклади розв’язання задач з астрономії Приклади розв’язання задач з астрономії § 1. Зоря Вега розташована на відстані 26,4 св. року від Землі. Скільки років летіла б до неї ракета з...

  5. Вивчення Всесвіту за допомогою космічних апаратів § 6. Методи астрофізичних досліджень 6. Вивчення Всесвіту за допомогою космічних апаратів Із початком космічної ери настає новий етап вивчення Всесвіту за допомогою ШСЗ та...

  6. Антропний принцип § 17. Життя у Всесвіті 1. Антропний принцип Життя є однією з великих таємниць Всесвіту. Ми бачимо на Землі різноманітні живі організми, але нічого не...

  7. Предмет астрономії § 1. Що вивчає астрономія 1. Предмет астрономії Назва астрономія походить з грецької мови (astron – зоря, nomos – закон), тобто це наука, яка вивчає...

  8. Юпітер §9. Планети-гіганти 2. Юпітер Юпітер, який був названий на честь наймогутнішого бога римської міфології, виявився найбільшою планетою Сонячної системи. Основними компонентами атмосфери Юпітера є водень...

  9. Закон всесвітнього тяжіння § 4. Закони руху планет 4.Закон всесвітнього тяжіння Великий англійський фізик і математик Ісаак Ньютон довів, що фізичною основою законів Кеплера є фундаментальний закон всесвітнього...

  10. Нові та Наднові зорі §14. Еволюція зір 4.Нові та Наднові зорі Зорі з масою у кілька разів більшою, ніж сонячна, закінчують своє життя грандіозним вибухом. У 1054 р. китайські...

  11. Телескопи § 6. Методи астрофізичних досліджень 4. Телескопи На жаль, більшість космічних об’єктів ми не можемо спостерігати неозброєним оком, бо його можливості обмежені. Телескопи (грец. tele...

  12. Головні ери в історії Всесвіту § 16. Еволюція Всесвіту 2.Головні ери в історії Всесвіту Всесвіт на початку існування мав настільки маленькі розміри, що тоді не було ні галактик, ні зір...

  13. Практичне використання космонавтики § 5. Основи космонавтики 6. Практичне використання космонавтики У наш час космонавтика використовується не тільки для вивчення Всесвіту, але й приносить велику практичну користь людям...

  14. Фізичні характеристики Сонця §12. Сонце – наша зоря 1. Фізичні характеристики Сонця Сонце – одна з мільярдів зір нашої Галактики, центральне світило в Сонячній системі, вік якого близько...

  15. Майбутнє Всесвіту § 16. Еволюція Всесвіту 4. Майбутнє Всесвіту Гравітаційна взаємодія речовини в майбутньому може зменшити швидкість розширення Всесвіту. Виявляється, якщо середня густина Всесвіту має критичне значення...

  16. Життя як відкрита система, яка зберігає та передає інформацію з минулого в майбутнє § 17. Життя у Всесвіті 2. Життя як відкрита система, яка зберігає та передає інформацію з минулого в майбутнє Загальні характеристики живих істот можна описати...

  17. Уран §9. Планети-гіганти 4.Уран Названий на честь бога неба Уран є по-справжньому блакитною планетою, тому що одну сьому його атмосфери складає метан. Існує одна особливість, яка...

  18. Коротка історія астрономії § 1. Що вивчає астрономія 2. Коротка історія астрономії З давніх-давен небо вражало уяву людей своєю загадковістю, але багато століть воно залишалось для них недосяжним,...

  19. Точки та лінії небесної сфери § 2. Основи практичної астрономії 2. Точки та лінії небесної сфери На небесній і земній сферах можна провести деякі кола, за допомогою яких визначаються небесні...

  20. Кільця Сатурна § 10. Супутники планет 4. Кільця Сатурна Кільця Сатурна (рис. 10.7) уперше побачив Галілей у 1610 p., але за допомогою невеликого телескопа він не зміг...

  21. Великий Вибух та вік Всесвіту § 16. Еволюція Всесвіту 1.Великий Вибух та вік Всесвіту Астрономічні дослідження, що проводились у XX ст., допомогли астрономам збагнути розлітання галактик, яке свідчить про те,...

  22. Друга і третя космічні швидкості § 5. Основи космонавтики 5. Друга і третя космічні швидкості Друга і третя космічні швидкості визначають умови відповідно для міжпланетних і міжзоряних перельотів. Якщо порівняти...

  23. Небесна сфера § 2. Основи практичної астрономії 1.Небесна сфера Під час спостережень за зорями нам здається, що всі небесні світила розташовані на однаковій відстані, ніби світять на...

  24. Вплив сонячної активності на Землю §12. Сонце – наша зоря 4. Вплив сонячної активності на Землю Досліджуючи Сонце за допомогою супутників та АМС, астрономи виявили його сильне корпускулярне випромінювання –...

  25. Планети земної групи та планети-гіганти § 7. Земля і Місяць 1. Планети земної групи та планети-гіганти Планети Сонячної системи за розмірами і будовою діляться на дві групи – планети земної...

  26. Супутники Юпітера § 10. Супутники планет 2. Супутники Юпітера Юпітер має принаймні 63 супутники, які були зареєстровані до 2011 p., і тьмяні кільця. Чотири найбільші супутники: Іо,...

  27. Астероїди §11. Малі тіла Сонячної системи 1. Астероїди Перший астероїд (від грец.- зореподібний) відкрив італійський астроном Д. Піацці (1746-1826). У ніч на 1 січня 1801 р....

  28. “Сім’я” Сатурна § 10. Супутники планет 3. “Сім’я” Сатурна “Сім’я” Сатурна складається із системи кілець і 62 супутників, які були відкриті до 2011 p., але більшість із...

  29. Прогнози еволюції земної цивілізації § 17. Життя у Всесвіті 5. Прогнози еволюції земної цивілізації Час існування окремої цивілізації теж впливає на визначення загальної кількості цивілізацій у Галактиці. Наприклад, у...

  30. Рух космічних апаратів по еліптичних орбітах § 5. Основи космонавтики 3. Рух космічних апаратів по еліптичних орбітах Якщо величина швидкості супутника буде відрізнятися від колової або вектор швидкості не буде паралельним...

  31. Видимі зоряні величини §13. Фізичні характеристики зір 2. Видимі зоряні величини Уперше термін “зоряна величина” був уведений для визначення яскравості зір грецьким астрономом Гіппархом у II ст. до...

  32. Сидеричний і синодичний періоди обертання планет § 4. Закони руху планет 2. Сидеричний і синодичний періоди обертання планет Сидеричний період обертання визначає рух тіл відносно зір. Це час, протягом якого планета,...

  33. Сонячний час та зодіак § 3. Вимірювання часу та календар 2. Сонячний час та зодіак Слово зодіак (від грец.- коло із зображень тварин) уперше почали вживати для визначення особливих...

  34. Зародження космонавтики § 5. Основи космонавтики 1. Зародження космонавтики Космонавтика вивчає рух штучних супутників Землі (ШСЗ), космічних кораблів і міжпланетних станцій у космічному просторі. Існує одна суттєва...

  35. Фізичні умови на Місяці § 7. Земля і Місяць 5. Фізичні умови на Місяці Не дивлячись на те, що Місяць розміщений майже на такій самій відстані від Сонця, як...

Визначення відстаней до планет