Тема. Дроби. Порівняння дробів. Складені задачі, які включають знаходження частини числа (№№ 760-769).
Мета. Ознайомити учнів з поняттями “чисельник” і “знаменник”; вчити записувати і закріплювати вміння розв’язувати задачі на знаходження частини числа; розвивати логічне мислення учнів.
Обладнання. Таблиця “Порівняння дробів”; завдання для опитування; короткий запис і план розв’язування задачі.
Зміст уроку
I. Контроль, корекція і закріплення знань.
1. Перевірка домашнього завдання.
А) Пояснити розв’язання
(280 : 4 – 150 : 3 = 20 (н.).)
Б) Зачитати відповідь до задачі № 759.
(Відповідь: відстань КМ на 60 км менша, ніж половина відстані КО.)
2. Усні обчислення.
А) Порівняти частини: 
і 
; 
і 
; 
і 
; 
і 
Б) Назвати частини в порядку спадання:
, , , , , ,
В) Знайти у від 1 кг (= 250г); від 2 діб (= 12 год); від 1 року (= 4міс.).
Г) Марійка прочитала 12 сторінок книжки, що становить у всієї книжки. Скільки всього сторінок має книжка? (48с.) Скільки сторінок книжки Марійці залишилося прочитати? (36 с.)
Г) Довжина стрічки дорівнює 30 см. Від усієї стрічки відрізали 80 см. Скільки сантиметрів стрічки залишилося? (100 см)
3. Завдання для опитування.
1) 3 ділянки учні зібрали 120 кг помідорів і 210 кг огірків. Четверту частину помідорів і третю частину огірків віддали у дитячий садок. Скільки кілограмів овочів віддали у дитячий садок? (Відповідь: 100 кг.)
2) Знайти 
від 840. Розв’язання записати. (120)
II. Вивчення нового матеріалу.
1. Підготовчі вправи.
Виконання завдань №№ 760, 761.
2. Пояснення (за таблицею).
Поява частин , , і т. д. зумовлена потребою поділити ціле на частини. Проте основною причиною виникнення частин є процес вимірювання величин.
Результат вимірювання не завжди можна виразити натуральним числом. Вважається, що спочатку існували лише двійкові частини: , , , 
, 
.
Були поширені також частини: половина – , чверть – , півчверть – , півпівчверть – , третина – півтретини – .
Такі числа називають дробовими.
Число над рискою (чисельник) показує, скільки рівних частин цілого взято; число під рискою (знаменник) показує, на скільки рівних частин поділено ціле число.
Наприклад: 
; 2 – чисельник; 3 – знаменник.
3. Первинне закріплення вивченого.
А) Читання дробів.
; 
; 
; 
; 
.
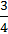– Що означає кожний дріб?
(Ціле поділили на 4 рівні частини і взяли таких З частини і т. д.)
Б) Вправа № 762 (усно).
В) Виконання завдань №№ 763, 764, 765 (з коментуванням).
Фізкультхвилинка.
III. Розвиток математичних знань.
1. Розв’язування задач.
А) Задача № 766.
Учні розв’язують задачу самостійно, а потім здійснюють взаємоперевірку.
(Розв’язання: 2 т 4 ц =24 ц
1) 24 : 3 = 8 (ц) – придбав ресторан;
2) 24 – 8 = 16 (ц) – розфасували в пакети;
3) 1600 : 4 = 400 (п.).)
Відповідь: 400 пакетів із крупами.)
Б) Задача № 767*.
(Розв’язання:
1) 60 : 3 = 20 (хв) – витратив учень, щоб пройти 1 км;
2) 1 км : 20 = 1000 м : 20 = 30 (м/хв) – швидкість учня;
3) 50 • 3 = 150 (м) – пройде учень за 3 хвилини;
4) 300 – 150 = 150 (м) – залишилося пройти.)
Отже, учень не встигне своєчасно прийти до школи, якщо буде йти з тією самою швидкістю.
IV. Підсумок уроку.
– Прочитайте дроби: 
; 
– Назвіть чисельники (знаменники).
V. Домашнє завдання.
№№ 768, 769 (с. 126).
(2 votes, average: 5,00 out of 5)