Урок № 2
Тема. Опуклі чотирикутники. Сума кутів чотирикутника
Мета: сформувати уявлення про внутрішню область чотирикутника, поняття опуклого та неопуклого чотирикутників, кута опуклого чотирикутника, сусідніх та протилежних кутів опуклого чотирикутника. Сформувати первинні вміння:
– відтворювати вивчені означення;
– розрізняти на готових рисунках вивчені об’єкти;
– зображувати вивчені об’єкти на рисунку.
Сформувати усвідомлене розуміння змісту теореми про суму кутів опуклого чотирикутника
Тип уроку: засвоєння нових знань.
Наочність та обладнання: конспект “Чотирикутники”.
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Для перевірки засвоєння учнями змісту основних понять, розглянутих на попередньому уроці, можна провести математичний диктант.
Математичний диктант
Варіант 1 | Варіант 2 |
1. Виконайте зображення чотирикутника MNKP | STOR |
Позначте на рисунку пару протилежних сторін | Протилежних |
2. Як називаються відрізки, що з’єднують протилежні вершини чотирикутника? | 2. Чим є в чотирикутнику кінці його діагоналі? |
3. Які з вершин чотирикутника АМОР є сусідніми до вершини А? | 3. Які зі сторін чотирикутника ВСКМ є сусідніми до сторони КМ? |
4. Одна зі сторін чотирикутника удвічі більша від кожної з інших сторін. Знаючи, що периметр чотирикутника дорівнює 40 см, знайдіть довжину | Утричі менша |
Більшої зі сторін | Меншої зі сторін |
III. Формулювання мети і завдань уроку
З метою кращого усвідомлення учнями навчального матеріалу уроку доцільно використати прийом аналогії. Для цього порівняємо означення трикутника та його елементів з означенням чотирикутника та його елементів. Під час порівняння означень повторюємо означення внутрішнього кута трикутника та теорему про суму всіх його кутів. Отже, виникає питання про існування аналогічної теореми про суму внутрішніх кутів чотирикутника. Відповідь на це питання і є основною дидактичною метою уроку.
IV. Актуалізація опорних знань
Виконання усних вправ за готовими рисунками
1. |
| Дано: АВ = ВС, AD = DC. Довести: |
2. |
| Дано: АD || ВС. Довести: |
3. |
| Дано: Довести: AB = AD, BC = CD |
4. |
| Дано: АВ = АD, СB = СD. Довести: AC |
5. |
| Дано: AB = DC, ВС = AD. Довести: |
V. Засвоєння знань
План вивчення нового матеріалу
1. Внутрішня область чотирикутника.
2. Опуклий чотирикутник.
3. Внутрішній кут опуклого чотирикутника.
4. Властивість внутрішніх кутів опуклого чотирикутника.
@ Під час підготовки до викладення матеріалу щодо поняття опуклого чотирикутника за новим підручником учителю слід звернути увагу на інший підхід до викладення цього питання, а саме: спочатку вводиться поняття внутрішньої області чотирикутника (надалі використовується для введення поняття площі многокутника), а потім формується уявлення про два можливих випадки взаємного розташування прямої, що містить сторону чотирикутника, відносно внутрішньої області чотирикутника: пряма або перетинає, або не перетинає цю внутрішню область. Далі на основі цього уявлення формується поняття опуклого (і неопуклого) чотирикутника, яке закріплюється під час роботи за готовими рисунками. Що стосується поняття кута опуклого чотирикутника (внутрішнього), а також теореми про суму кутів опуклого чотирикутника, то ці питання в новому підручнику висвітлюються за такими ж принципами, як і в традиційних підручниках геометрії (як, зокрема, у підручнику Геометрія. 7-9 / Під ред. О. В. Погорєлова).
Завдання. На якому з наведених рисунків зображено опуклий чотирикутник (див. рис. 1)?

VI. Формування вмінь та навичок
Виконання усних вправ
1. Чи можуть усі кути опуклого чотирикутника бути гострими? тупими? прямими?
2. Чи може опуклий чотирикутник мати три гострі кути? три тупі кути? два прямі кути? три прямі кути і один непрямий?
3. Чи можуть кути трикутника дорівнювати трьом кутам чотирикутника? Відповідь обгрунтуйте.
Виконання графічних вправ
Проведіть дві паралельні прямі. Позначте на одній з них точки А і D, а інші – точки В і С, так, щоб за послідовного сполучення цих точок утворився чотирикутник ABCD.
А) Чи є побудований чотирикутник опуклим? Чому?
Б) Виміряйте зовнішні кути чотирикутника ABCD (по одному при кожній вершині) та обчисліть їх суму.
Виконання письмових вправ
1. Два кути чотирикутника дорівнюють 80° і 100°, а два інші кути мають рівні градусні міри. Знайдіть найбільший кут чотирикутника.
2. Знайдіть кути чотирикутника, якщо один із них удвічі менший від другого, на 20° менший від третього і на 40° менший від четвертого.
3. Периметри чотирикутників ABCD і ABCD1 рівні. Чи може один із цих чотирикутників бути опуклим, а другий – неопуклим? Відповідь підтвердьте рисунком.
VII. Підсумки уроку
Завдання. У наведених твердженнях знайдіть та виправте помилку:
1) сума кутів будь-якого чотирикутника дорівнює 360°;
2) чотирикутником називається фігура, яка складається з чотирьох точок, жодні три з яких не лежать на одній прямій, і чотирьох відрізків, які послідовно сполучають ці точки;
3) діагональ чотирикутника – це відрізок, що з’єднує дві вершини чотирикутника;
4) опуклий чотирикутник – це чотирикутник, який не перетинається прямою.
VIII. Домашнє завдання
Вивчити зміст понять, розглянутих на уроці (див. конспект), та доведення теореми про суму кутів опуклого чотирикутника. Розв’язати задачі.
1. Знайдіть кути чотирикутника ABCD, якщо 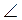 A =
A = 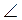 B,
B, 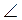 C =
C = 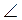 D, а сума кутів А і В дорівнює 160°.
D, а сума кутів А і В дорівнює 160°.
2. Знайдіть найменший кут чотирикутника, якщо суми його кутів, узятих по три, дорівнюють 240°, 260° і 280°.
3. Якщо один із кутів опуклого чотирикутника – гострий, то в цьому чотирикутнику обов’язково є тупий кут. Доведіть.




 BD
BD

