Електроємність. Енергія електричного поля

ЕЛЕКТРОДИНАМІКА

Електричне поле. Електричний струм

УРОК 4/4

Тема. Електроємність. Енергія електричного поля

Мета уроку: ознайомити учнів з поняттям електричної ємності провідника.

Тип уроку: урок вивчення нового матеріалу.

ПЛАН УРОКУ

Контроль знань	5 хв.	1. Що називають потенціалом електричного поля? 2. Що таке різниця потенціалів? 3. Принцип суперпозиції 4. Зв’язок між різницею потенціалів і напруженістю
Демонстрації	3 хв.	1. Неоднакова зміна потенціалу двох ізольованих провідників різного розміру у разі передання їм однакових зарядів. 2. Вирівнювання потенціалів заряджених провідників різного розміру
Вивчення нового матеріалу	27 хв.	1. Поняття електроємності. 2. Одиниця електроємності. 3. Конденсатори. 4. Енергія електричного поля
Закріплення вивченого матеріалу	10 хв.	1. Якісні питання. 2. Навчаємося розв’язувати задачі.

ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ

1. Поняття електроємності

Для введення

поняття електроємності можна поставити ряд дослідів, на яких треба показати неоднакову зміну потенціалу двох ізольованих провідників різного розміру під час передання їм рівних зарядів і продемонструвати далі, що для одержання рівних потенціалів цим провідникам потрібні неоднакові заряди.

1-й дослід. За допомогою пробної кульки з електрофорної машини переносять на кожну з куль однакову кількість електрики.

За показаннями електрометрів з’ясовують, що потенціал малої кулі з кожною порцією перенесеного заряду збільшувався швидше й досяг більшої величини, ніж у великої (див. рис. 1). Це відбувається подібно до того, як рівень рідини у вузькій циліндричній посудині підвищується швидше й досягає більшої висоти, ніж у широкій, якщо налити в них однакову кількість рідини (див. рис. 2).

Рис. 1

Рис. 2

2-й дослід. Заряджені кулі з’єднують провідником. За показаннями електрометрів видно, що потенціали куль стали рівними. Після з’єднання відбувалося переміщення заряду у бік зниження потенціалу, тобто від малої кулі до більшої, поки потенціали не вирівнялися. Отже, тепер на кулях заряди не рівні; у великої кулі заряд більший, ніж у малої.

Це аналогічно явищу, що відбувається під час з’єднання двох посудин різного поперечного перерізу, у яких рівні рідини спочатку перебувають на різній висоті, а після з’єднання вирівнюються (див. рис. 3).

Рис. 3

Виконані досліди показують, що в кожного провідника потенціал змінюється пропорційно заряду, а відношення заряду до потенціалу q/? для даного провідника – величина постійна, яка залежить від його розмірів і форм і називається електроємністю провідника:

Аналогічно, у кожній з посудин висота змінюється пропорційно об’єму налитої рідини, але відношення об’єму рідини до висоти також є величиною постійною, що характеризує властивість посудини – її ємність і дорівнює площі її поперечного перерізу:

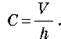
O Отже, відношення заряду q відокремленого провідника до його потенціалу?, тобто величину називають електроємністю цього провідника.

2. Одиниці електроємності

Одиницею електроємності в СІ є [С] = 1 Кл/1 В = 1 Ф. На честь англійського фізика М. Фарадея ця одиниця названа фарадом.

O 1 фарад – ємність провідника, у якого зміна заряду на 1 Кл спричиняє зміну потенціалу на 1 В.

Для практичних цілей використовують малі частинки фарада: 1 мкФ = 10-6 Ф; 1 пФ = 10-12 Ф.

3. Конденсатори

Величина електроємності залежить від форми й розмірів провідників і від властивостей діелектрика, що розділяє провідники. Існують такі конфігурації провідників, за яких електричне поле виявляється зосередженим (локалізованим) лише в деякій області простору. Такі системи називаються конденсаторами, а провідники, що входять до складу конденсатора, називаються обкладками.

Конденсатор – це два провідники, що мають рівні й протилежні за знаком заряди, причому конфігурація провідників така, що створюване ними поле зосереджено в основному між провідниками.

Чим більша ємність, тим більший заряд можна помістити на обкладки конденсатора за тієї ж різниці потенціалів між ними. Виходить, електроємність характеризує здатність двох провідників накопичувати електричний заряд.

Найпростіший конденсатор – система із двох плоских провідних пластин, розташованих паралельно один до одного на малій порівняно з розмірами пластин відстані й розділених шаром діелектрика. Такий конденсатор називається плоским.

Електроємність плоского конденсатора визначають виразом:

Де S – площа кожної пластини, a d – відстань між пластинами. Величину?0 називають електричною сталою:

4. Енергія електричного поля

Якщо на обкладках конденсатора електроємністю С розміщено електричні заряди +q й – q, то напруга між обкладками конденсатора дорівнює: U = q/С. Під час розряджання конденсатора напруга між його обкладками убуває прямо пропорційно заряду q від первинного значення U до 0. Середнє значення напруги упродовж розряджання дорівнює:

Для роботи А, здійснюваної електричним полем під час розряджання конденсатора, будемо мати:

Отже, потенціальна енергія Wp конденсатора електроємністю С, зарядженого до напруги U, дорівнює:

Енергія конденсатора обумовлена тим, що електричне поле між його обкладками має енергію. Напруженість Е поля пропорційна до напруги U, тому енергія електричного поля пропорційна до квадрата його напруженості.

Отже, ми знайшли, чому дорівнює енергія зарядженого конденсатора, розглядаючи її як потенціальну енергію заряджених пластин. Де ж зосереджена ця енергія? Розводячи пластини конденсатора, ми виконуємо роботу, збільшуючи об’єм простору, який займає електричне поле. Тому потенціальна енергія взаємодії заряджених пластин – це енергія електричного поля, тому що це поле виникло саме під час розведення пластин.

ПИТАННЯ ДО УЧНІВ У ХОДІ ВИКЛАДУ НОВОГО МАТЕРІАЛУ

Перший рівень

1. Від чого залежить електроємність?

2. Чи залежить електроємність відокремленого провідника від його розмірів й форми?

3. Чи залежить електроємність відокремленого провідника від наявності поблизу нього інших провідників?

4. Що відбудеться з різницею потенціалів на пластинах зарядженого конденсатора, якщо зменшити відстань між ними?

5. Що відбудеться з різницею потенціалів на пластинах зарядженого конденсатора, якщо площу пластин збільшити?

Другий рівень

1. Дві однакові провідні відокремлені кулі у вакуумі набули різних зарядів. Що можна сказати про потенціали куль?

2. За допомогою якого досліду можна переконатися в тому, що заряджений конденсатор має енергію?

3. Чи можна збільшити енергію зарядженого розсувного конденсатора, не змінюючи різниці потенціалів на його пластинах?

4. Яку небезпеку являють собою знеструмлені кола з наявними в них конденсаторами?

ЗАКРІПЛЕННЯ ВИВЧЕНОГО МАТЕРІАЛУ

1). Якісні питання

1. Чи справедливим є твердження, що під зарядом конденсатора розуміють суму зарядів його обкладок?

2. У скільки разів зміниться ємність плоского конденсатора, якщо збільшити робочу площу пластин в 2 рази?

3. Відстань між пластинами плоского конденсатора збільшили в 4 рази. Як змінилася ємність конденсатора?

4. Пластини плоского конденсатора розсовують. У якому випадку доведеться виконати більшу роботу:

А) конденсатор увесь час підключений до джерела напруги;

Б) конденсатор відімкнений від джерела після заряджання?

2). Навчаємося розв’язувати задачі

1. Коли конденсатор підключили до джерела постійної напруги, одна з його обкладок набула заряду 20 нКл. Чому дорівнює:

А) заряд конденсатора;

Б) сумарний заряд обох обкладок?

(Відповідь: а) 20 нКл; б) 0).)

2. Який заряд потрібно передати конденсатору ємністю 6 мкФ, щоб різниця потенціалів між його пластинами дорівнювала 25 В?

(Відповідь: 0,15 мКл.)

3. Яка кількість теплоти виділиться в провіднику під час розряджання через нього конденсатора ємністю 100 мкФ, зарядженого до різниці потенціалів 1,2 кВ?

(Відповідь: 72 Дж.)

ЩО МИ ДІЗНАЛИСЯ НА УРОЦІ

– Відношення заряду q відокремленого провідника до його потенціалу? називається електроємністю цього провідника:

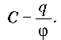
– Фарад – ємність провідника, у якого зміна заряду на 1 Кл спричиняє зміну потенціалу на 1 В.

– Конденсатор – два провідники, що мають рівні й протилежні за знаком заряди, причому конфігурація провідників така, що поле, створюване ними, зосереджено в основному між провідниками.

– Електроємність плоского конденсатора:

– Енергія зарядженого конденсатора:

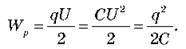
Домашнє завдання

1. Підр.: § 4.

2. 3б.:

Рів1 № 3.11; 3.12; 3.13; 3.14.

Рів2 № 3.24; 3.25; 3.26, 3.27.

Рів3 № 3.44, 3.46; 3.47; 3.50.

3. Д: підготуватися до самостійної роботи № 2.