Геометрія
Стереометрія
Перпендикулярність прямих і площин
Дві прямі називаються Перпендикулярними, якщо вони перетинаються під прямим кутом.
Теорема 1. Якщо дві прямі, які перетинаються, паралельні відповідно двом іншим перпендикулярним прямим, то інші прямі теж перпендикулярні.
Теорема 2. Через будь-яку точку прямої у просторі можна провести безліч перпендикулярних до неї прямих (див. рисунок). (Усі прямі лежать у площині, яка перпендикулярна до даної прямої і перетинає її у даній точці.)
Зверніть увагу, що в просторі дві прямі, перпендикулярні до однієї і тієї самої прямої, не обов’язково паралельні між собою.
На рисунку 
; 
.
Пряма, яка перетинає площину, називається Перпендикулярною до цієї площини, якщо вона перпендикулярна
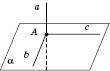
Теорема 3. Якщо пряма перпендикулярна до двох прямих, які лежать у площині й перетинаються, то вона перпендикулярна до даної площини (див. рисунок).
Зверніть увагу: якщо пряма перпендикулярна до однієї прямої площини, то цього не досить для перпендикулярності прямої і площини.
На рисунку 
, але a не перпендикулярна до 
, зокрема a не перпендикулярна до с.
Теорема 4. Через точку, яка не належить даній площині, можна провести пряму, перпендикулярну до даної площини, і тільки одну.
Теорема 5. Через дану точку площини можна провести одну, й тільки одну, перпендикулярну до неї пряму.
Теорема 6. Через дану точку прямої можна провести одну, й тільки одну, перпендикулярну до неї площину.
Теорема 7. Через точку, яка не лежить на прямій, можна провести одну, й тільки одну, площину, перпендикулярну до даної прямої.
Теорема 8. Якщо площина перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна й до другої.
На рисунку 
; 
; 
.
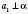Теорема 9. Дві прямі, перпендикулярні до однієї й тієї самої площини, паралельні.
(1 votes, average: 5,00 out of 5)