УРОК № 60
Тема. Тематична контрольна робота № 7
Мета уроку: перевірка навчальних досягнень учнів з курсу геометрії.
Тип уроку: контроль навчальних досягнень учнів.
Вимоги до рівня підготовки учнів: застосовують означення та властивості фігур при розв’язуванні задач.
Хід уроку
І. Тематичне оцінювання № 7
Тематичне оцінювання № 7 можна провести у вигляді тематичної контрольної роботи. Наводимо текст контрольної роботи. Кожна правильна відповідь оцінюється в 3 бали.
Варіант 1
1. Бічна сторона гострокутного
 –
–  |, якщо |
|, якщо | | = 7, |
| = 7, | | = 8, a кут між векторами
| = 8, a кут між векторами  і
і  дорівнює 120°.
дорівнює 120°.Варіант 2
1. Основа гострокутного рівнобедреного трикутника дорівнює 30 см, а висота, опущена
 +
+  |, якщо |
|, якщо | | = 7, |
| = 7, | | = 8, а кут між векторами
| = 8, а кут між векторами  і
і  дорівнює 60°.
дорівнює 60°.Варіант 3
1. Периметр рівнобедреного трикутника дорівнює 80 см, а висота, опущена на основу,- 20 см. Знайдіть основу трикутника. 2. Сторона ромба дорівнює 12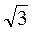 см, а тупий кут становить 120°. Знайдіть діагоналі ромба. 3. Точка дотику вписаного у прямокутний трикутник круга ділить гіпотенузу на відрізки завдовжки 8 см і 12 см. Знайдіть площу вписаного круга. 4. Знайдіть |
см, а тупий кут становить 120°. Знайдіть діагоналі ромба. 3. Точка дотику вписаного у прямокутний трикутник круга ділить гіпотенузу на відрізки завдовжки 8 см і 12 см. Знайдіть площу вписаного круга. 4. Знайдіть | –
–  |, якщо |
|, якщо | | = 3, |
| = 3, | | = 8, а кут між векторами
| = 8, а кут між векторами  і
і  дорівнює 60°.
дорівнює 60°.
Варіант 4
1. Периметр рівнобедреного трикутника дорівнює 160 см, а висота, опущена на його основу,- 40 см. Знайдіть бічну сторону трикутника. 2. Діагоналі ромба дорівнюють 12 см і 12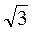 см. Знайдіть гострий кут ромба. 3. Точка дотику вписаного в прямокутний трикутник кола ділить його гіпотенузу у відношенні 2 : 3. Катет дорівнює 12 см. Знайдіть площу вписаного круга. 4. Знайдіть |
см. Знайдіть гострий кут ромба. 3. Точка дотику вписаного в прямокутний трикутник кола ділить його гіпотенузу у відношенні 2 : 3. Катет дорівнює 12 см. Знайдіть площу вписаного круга. 4. Знайдіть | +
+  |, якщо |
|, якщо | | = 5, |
| = 5, | | = 8, а кут між векторами а і b становить 120°.
| = 8, а кут між векторами а і b становить 120°.
Розв’язання та відповіді до завдань тематичної контрольної роботи № 7
Варіант 1
1. Відповідь. 80 см.
2. Відповідь. 24 см.
3. Нехай трикутник ABC прямокутний, АО = 10 см, ВС = 16 см (рис. 301).
Із прямокутного трикутника ABC маємо: АС = =
= = 12 (см). r =
= 12 (см). r =  =
=  = 4(см). Sкр = nr2 = n? 42 = 16n (cм2).
= 4(см). Sкр = nr2 = n? 42 = 16n (cм2).
Відповідь. 16n см2.
4. Нехай ВА = 7, ВС = 8,  ABC = 120° (рис. 302).
ABC = 120° (рис. 302).
| –
–  | = АС =
| = АС =  =
=  =
=  = 13.
= 13.
Відповідь. 13.

Варіант 2
1. Відповідь. 80 см.
2. Відповідь. 30 і 40 см.
3. Нехай у прямокутний трикутник ABC ( A = 90°) вписано коло; М, N, К – точки дотику, OM = ON = OK = 4 см, АВ = 12 см (рис. 303).
A = 90°) вписано коло; М, N, К – точки дотику, OM = ON = OK = 4 см, АВ = 12 см (рис. 303).
Тоді ВМ = АВ – АМ = 12 – 4 = 8 (см), ВК = 8 см.
Нехай КС = х см. Тоді ВС = х + 8, АС = х + 4 і з трикутника ABC маємо:
(х + 8)2 = (х + 4)2 + 122; х2 + 16х + 64 = х2 + 8х + 16 + 144; 8х = 96, х = 12. Отже, ВС = 12 + 8 = 20 (см). S = nR2 = n?  = n? 102 = 100n (см2).
= n? 102 = 100n (см2).
Відповідь. 100n см2.

4. Нехай | | = АВ = 7, |
| = АВ = 7, | | = AD = 8,
| = AD = 8,  BAD = 60° (рис. 304), тоді
BAD = 60° (рис. 304), тоді  ABC = 180° – 60° = 120°. Із трикутника ABC маємо:
ABC = 180° – 60° = 120°. Із трикутника ABC маємо:
| +
+  | = АС =
| = АС =  =
=  =
=  = 13.
= 13.
Відповідь. 13.

Варіант 3
1. Відповідь. 30 см.
2. Відповідь. 12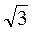 См і 36 см.
См і 36 см.
3. Нехай у прямокутний трикутник ABC вписано круг, М, L, К – точки дотику; BL = 8 см, CL = 12 см (рис. 305). ВК = KL = 8 см, LC = MC = 12 см.
Нехай АК = х см, тоді АМ = х см. Отже, із трикутника ABC маємо:
(х + 8)2 + (х + 12)2 = 202; х2 + 16х + 64 + х2 + 24х + 144 = 400;
2х2 + 40х – 192 = 0, х2 + 20х – 96 = 0 , х = -24 або х = 4. х = -24 умову задачі не задовольняє, отже, х = 4 см. S = n? AM2 = n? 42 = 16n (см2).
Відповідь. 16n см2.

4. Нехай | | = АВ = 3, |
| = АВ = 3, | | = АО = 8,
| = АО = 8,  BAD = 60° (рис. 306).
BAD = 60° (рис. 306).
| –
–  | = BD =
| = BD =  =
=  =
=  = 7.
= 7.
Відповідь. 7.

Варіант 4
1. Відповідь. 50 см.
2. Відповідь. 60°.
3. Нехай у прямокутний трикутник ABC ( A = 90°) вписано коло; К, L, М – точки дотику, АВ = 12 см, BL : CL = 2 : 3 (рис. 307).
A = 90°) вписано коло; К, L, М – точки дотику, АВ = 12 см, BL : CL = 2 : 3 (рис. 307).
Нехай АК = х см, тоді ВК = 12 – х, BL = 12 – x, LC =  ? 3 = 18 – 1,5х,
? 3 = 18 – 1,5х,
BC = BL + LC = 30 – 2,5x, АС = х + 18 – 1,5х = 18 – 0,5х. Із прямокутного трикутника ABC маємо: (30 – 2,5х)2 = 122 + (18 – 0,5x)2;
900 – 150х + 6,25х2 = 144 + 324 – 18х + 0,25х2; 6х2 – 132х + 432 = 0, х2 – 22х + 72 = 0, х = 18 або х = 4.
Ураховуючи, що х < 12, маємо х = 4. Отже, ОК = 4 см. S = n? OK2 = 16n (см2).
Відповідь. 16n см2.

4. Нехай | | = АВ = 5, |
| = АВ = 5, | | = BC = 8,
| = BC = 8,  АВС = 120° (рис. 308).
АВС = 120° (рис. 308).
Тоді  BCD = 180° – 120° = 60°. Із трикутника BCD маємо:
BCD = 180° – 120° = 60°. Із трикутника BCD маємо:
| +
+  | = BD =
| = BD =  =
=  =
=  = 7.
= 7.
Відповідь. 7.

Тематичне оцінювання № 7 можна провести у вигляді тестового завдання. Кожне завдання І та II рівнів оцінюється 1 балом, ІІІ рівня – 2 балами, IV рівня – 3 балами.
При оцінюванні ураховуються тільки ті шість із виконаних завдань, яким відповідає найбільша кількість балів. Якщо учень набрав у сумі нецілу кількість балів, результат округлюється в бік збільшення; якщо більше 12 балів – отримує 12 балів.
Тестова робота
І рівень
1. У прямокутному трикутнику ABC ( B = 90°) проведено меді ану ВМ (рис. 309). Виберіть правильне твердження.
B = 90°) проведено меді ану ВМ (рис. 309). Виберіть правильне твердження.
A.  A +
A +  C = 90°;
C = 90°;
Б. М – центр кола, вписаного в трикутник ABC;
В. АМ > ВМ.

2. Якщо діаметр АВ кола з центром у точці О утворює з хордою ВС кут 45° (рис. 310), то градусна міра кута АОС дорівнює:
А. 45°; Б. 60°; В. 90°.

3. Якщо ABCD – прямокутник (рис. 311), то:
A. AC BD;
BD;
Б. АС2 > АВ2 + ВС2;
В.  АСВ
АСВ 
 ACD.
ACD.

ІІ рівень
4. Укажіть рівняння кола, зображеного на рис. 312.
A. (x – 1)2 + y2 = 1;
Б. х2 + (у – 1)2 = 1;
В. (x + 1)2 + y2 = 1.

5. Якщо квадрат описаний навколо кола радіуса r, то площа квадрата дорівнює:
А. r2; Б. 2r2; В. 4r2.
6. Якщо круг вписаний у квадрат зі стороною 2а, то площа круга дорівнює:
А.  ; Б. nа2; В. 2nа2.
; Б. nа2; В. 2nа2.
III рівень
7. Гіпотенуза прямокутного трикутника дорівнює 10 см, а один із катетів дорівнює 6 см. Знайдіть площу трикутника.
А. 24 см2; Б. 48 см2; В. 60 см2.
8. Проекції катетів прямокутного трикутника на гіпотенузу відповідно дорівнюють 9 см і 16 см. Знайдіть менший катет трикутника.
А. 12 см; Б. 15 см; В. 20 см.
9. Знайдіть площу ромба, сторона якого дорівнює 13 см, а різниця діагоналей становить 14 см.
А. 60 см2; Б. 120 см2; В. 240 см2.
IV рівень
10. У трикутнику два кути становлять 120° і 30°, а прилегла до них сторона дорівнює 10 см. Знайдіть висоту трикутника, проведену до сторони завдовжки 10 см.
А. 5 см; Б. 5 см; В. 5
см; В. 5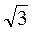 см.
см.
11. У ромб вписано коло. Сторона ромба точкою дотику ділиться на відрізки, довжини яких дорівнюють а і b. Знайдіть площу ромба.
А.  ; Б. 2
; Б. 2 ; В. 2
; В. 2 (а + b).
(а + b).
12. Точки А(-2; 0), В(2; 4), С(4; 2), D(0; -2) – вершини чотирикутника ABCD. Знайдіть координати центра кола, описаного навколо нього.
А. (2; 0); Б. (1; 0); B. (1; 1).
Відповіді до завдань тестової роботи
1. А. 2. В. 3. В. 4. Б. 5. В. 6. Б. 7. А. 8. Б. 9. Б. 10. В. 11. В. 12. В.
II. Домашнє завдання
Якщо в класі виконувалася тематична контрольна робота № 7, то вдома можна запропонувати виконати тест, і навпаки.
III. Підбиття підсумків уроку
З’ясувати, які завдання викликали труднощі в учнів, та відповісти на запитання учнів.


