1-й семестр
МЕХАНІКА
1. Кінематика
Урок 3/5
Тема. Відносність механічного руху
Мета уроку: розширити й поглибити знання про відносність руху; сформувати навички додавання швидкостей і переміщень, переходу від однієї системи відліку до іншої
Тип уроку: вивчення нового матеріалу
План уроку
Контроль знань | 5 хв. | 1. Прямолінійний рівномірний рух. 2. Переміщення в разі прямолінійного рівномірного руху. 3. Рівняння для координати в разі |
Демонстрації | 5 хв. | 1. Відносність стану спокою і руху. 2. Додавання переміщень. 3. Відео-фрагмент “Додавання переміщень і швидкостей” |
Вивчення нового матеріалу | 25 хв. | 1. Відносність руху. 2. Додавання переміщень і швидкостей. 3. Учимося розв’язувати задачі |
Закріплення вивченого матеріалу | 10 хв. | 1. Розв’язування задач. 2. Контрольні запитання |
ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ
1. Відносність руху
Нагадаємо учням, що система відліку
Можна поставити учням запитання: які ще кінематичні характеристики руху є відносними? На конкретних прикладах (плавець перепливає річку з одного берега на інший, рухаючись перпендикулярно до берегів; пасажир іде по вагону, що рухається, з’ясовуємо відносність переміщення і швидкості.
2. Додавання переміщень і швидкостей
Назвемо умовно одну систему відліку “нерухомою”, а іншу – “рухомою”. Тоді правило додавання переміщень можна сформулювати так:
O переміщення 
тіла в “нерухомій” системі відліку дорівнює векторній сумі переміщення 1 тіла в “рухомій” системі відліку й переміщення 2 “рухомої” системи відліку відносно “нерухомої” :
Поділивши співвідношення на час руху t, отримаємо закон додавання швидкостей: 
Це означає, що
O швидкість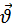 
тіла в “нерухомій” системі відліку дорівнює векторній сумі швидкості 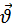1 тіла в “рухомій” системі відліку й швидкості 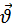2 “рухомої” системи відліку відносно “нерухомої”.
Важливо зазначити, що рух тіла відбувається в обох системах відліку одночасно. Відносно ж кожної системи тіло виконує у будь-який момент часу лише один рух.
3. Учимося розв’язувати задачі
Усвідомити й засвоїти досліджуваний матеріал учням допоможе розв’язування задач.
У повсякденному житті як тіло відліку ми часто сприймаємо Землю або яке-небудь інше тіло, пов’язане з нею. Однак у деяких випадках систему відліку зручно пов’язати з тілом, що рухається, тоді розв’язування багатьох задач на обчислення швидкості тіла відносно Землі спрощується. Для підтвердження цього можна розглянути два варіанти розв’язування наступної задачі.
Задача. Пропливаючи під мостом проти течії річки, весляр загубив капелюха. Виявивши пропажу за 10 хв., весляр повернув назад і підібрав капелюх на відстані d = 1 км нижче від моста. Обчисліть швидкість плину річки.
Розв’язування
1. Розв’яжемо задачу в системі відліку “Земля”.
Очевидно, що вгору проти течії човняр до виявлення пропажі проплив шлях 
Повернувши назад, він проплив відстань 
Час, за який він пропливе відстань l2, обчислимо як:
Загальний час руху весляра обчислюватиметься за формулою:
Капелюх за той же проміжок часу пройшов шлях 
звідки 
Тоді 
Тоді 
2. Розв’яжемо цю ж задачу в системі відліку “Вода”.
У цій системі відліку капелюх нерухомий. Швидкість човняра відносно води в обидва боки однакова; отже, і час t1 його руху від капелюха на деяку відстань, і час зворотного руху до капелюха t2 однакові. Тому t = t1 + t2 хв. За цей час місток “відійде” від капелюха на відстань d = 1 км.
Отже, 
Запитання до учнів під час викладу нового матеріалу
1. Велосипедист їде рівною прямою дорогою. Які деталі велосипеда рухаються відносно землі прямолінійними траєкторіями, а які – криволінійними?
2. Вітер несе повітряну кульку на південь. У який бік відхиляється прапорець, яким прикрашена кулька?
3. Річкою пливе весловий човен і поруч із ним – пліт. Що для весляра буде простішим: перегнати пліт на 1 м чи на стільки ж відстати від нього?
4. Які характеристики механічного руху змінюються внаслідок переходу від однієї системи відліку до іншої?
ЗАКРІПЛЕННЯ ВИВЧЕНОГО МАТЕРІАЛУ
1). Тренуємося розв’язувати задачі
1. Швидкість моторного човна відносно води становить 6 км/год., а швидкість течії ріки – 2 км/год. У скільки разів швидше човен рухається за течією, ніж проти течії?
2. Швидкість човна відносно води – 4 км/год., а швидкість течії – 2 км/год. За який час човен пройде 12 км за течією ріки? проти течії?
3. Велосипедист рухається зі швидкістю 25 км/год., а автомобіль – 55 км/год. З якою швидкістю рухається автомобіль відносно велосипедиста, якщо:
А) він рухається назустріч велосипедисту;
Б) наздоганяє його;
В) віддаляється від нього після обгону?
4. Плавець перепливає річку завширшки 150м, рухаючись зі швидкістю 2 м/с відносно води. Швидкість течії дорівнює 1 м/с.
А) Якими є швидкість і переміщення плавця відносно берега, якщо він рухається перпендикулярно плину ріки? Скільки часу необхідно плавцю, щоб переплисти річку? На яку відстань при цьому його знесе течією?
Б) Який час знадобиться плавцю, щоб переплисти річку, пропливаючи найменшу відстань відносно берега? Яким у цьому випадку буде його переміщення відносно води?
2). Контрольні запитання
1. Чи може людина, яка перебуває у вагоні потяга, що рухається, бути нерухомою відносно Землі?
2. Пасажир потяга, що рухається, дивився у вікно на зустрічний потяг, що проїжджав повз нього. Коли зустрічний потяг промчався, пасажиру здалося, що його потяг сповільнив хід. Чому?
3. Наведіть приклади, які підтверджують, що рух і стан спокою є відносними.
4. Чи завжди як нерухому систему відліку необхідно приймати ту, що пов’язана із Землею?
5. Чому дощові краплі в безвітряну погоду залишають похилі смуги на шибках автомобіля, що рухається рівномірно?
Що ми дізналися на уроці
– Переміщення тіла в “нерухомій” системі відліку дорівнює векторній сумі переміщення 1 тіла в “рухомій” системі відліку й переміщення 2 “рухомої” системи відліку відносно “нерухомої”:
– Швидкість 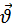тіла в “нерухомій” системі відліку дорівнює векторній сумі швидкості тіла 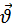1 в “рухомій” системі відліку і швидкості 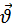2 “рухомої” системи відліку відносно “нерухомої”:
Домашнє завдання
1. П.:§8.
2. 36.:
P1) – 3.11; 3.14; 3.15; 3.17;
Р2) – 3.34; 3.36; 3.38, 3.39;
Р3) – 3.63, 3.64; 3.66; 3.67.
(2 votes, average: 4,00 out of 5)