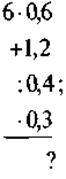Урок № 6 2
Тема. Додатні і від’ємні числа. Число 0
Мета: сформувати уявлення учнів про зміст понять “додатні числа”, “від’ємні числа”, а також виробити вміння відрізняти ці види чисел і виконувати прості вправи, що передбачають таку класифікацію.
Тип уроку: засвоєння нових знань.
Хід уроку
I. Актуалізація опорних знань
Усні вправи
1. Обчисліть: | А) |
| Б) |
| В) |
2. На рисунку зображено координатний промінь ОК. Знайдіть координати точок А, В, С, D, Е.
3. На рисунку зображено шкалу термометра, що вимірює температуру повітря. Яку температуру він показує за раз? Буде показувати, якщо стовпчик термометра підніметься на 3; на 7 поділок? Буде показувати, якщо стовпчик термометра спуститься на 2; на 5 поділок?
II. Формування знань
@ Формуючи уявлення учнів про додатні і від’ємні числа (як і в багатьох інших випадках) важливо спиратися на набутий шестикласниками життєвий
Звертаємо увагу на те, що спочатку краще наголосити, що число 0 на термометрі – це значення температури, при якій вода починає перетворюватися на кригу, і це число – межа між числами, що позначають більш теплу температуру (додатними), і числами, що позначають більш низьку температуру (від’ємними).
Тому всі числа умовно ділимо на: а) додатні; б) від’ємні; в) недодатне і невід’ємне, тобто 0.
Запис і читання додатних і від’ємних чисел зазвичай не викликає труднощів у учнів.
Більш складним, але дуже важливим для подальшого вивчення математики, є поняття “невід’ємне число”, “недодатне чиcло”.
III. Закріплення знань. Засвоєння вмінь
Усні вправи
1. Які з чисел: 4; -8; -11; 53;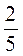 
; 
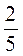; 0,4; -2,8; +4; + додатні? від’ємні? Які з них рівні між собою?
2. Провідміняйте “додатне число”, “від’ємне число”, “мінус двісті”, “мінус три сьомих”.
3. Назвіть за схемою розміщення точок на місцевості порівняно з рівнем океану (див. рис).
4. Чи правильно, що 0 невід’ємне число? Чи є число 0 недодатним?
Письмові вправи
Задача 1. Намалюйте схематично термометр, який показує -7 °С. Скільки градусів він показуватиме, якщо температура підвищиться на 4 °С? зміниться на 4 °С?
Задача 2. На географічних картах біля гори Говерла і берега Каспійського моря написано числа 2001 і -28. Що вони означають?
Задача 3. Гроші, які вносять до банку, касир записує зі знаком “+”, а які бере з банку – зі знаком “-“. Як змінилась сума грошей у касі після того, як касир обслужив 5 вкладників? (Див. таблицю)
Вкладник | Грошова операція |
1 | +300 |
2 | -250 |
3 | -200 |
4 | +700 |
5 | -400 |
Задача 4. У школу за рік поступило а учнів, а вибуло b учнів. На скільки змінилась кількість учнів школи за рік? Поясніть зміст відповіді, якщо:
А) а = 40; b = 23; б) а = 37; b = 45; в) а = 53; b = 53.
Задача 5. Чи може виражатися від’ємним числом:
А) кількість людей, що мешкає в будинку;
Б) довжина кімнати;
В) кількість грошей;
Г) маса якого-небудь предмета?
Задача 6 (на повторення). Обчисліть значення виразу:
А) 
;
Б) 
.
IV. Підсумки уроку
Які слова пропущені?
+3 | +7,5 |
| 0,5 | – додатні; |
-3 | -7,5 | – | -0,5 | – ? |
0 | 3 | +7,5 | – ? | |
-3 | 0 | -7,5 | – ? |
V. Домашнє завдання
Задача 1. Прочитайте числа: 4,2; -7; -8
; 1830; 0; -3,65; 6
. Які з них є: а) від’ємними; б) додатними; в) невід’ємними; г) недодатними?
Задача 2. Іра зайшла в ліфт дванадцятиповерхового будинку на сьомому поверсі. Проїхала 4 поверхи і вийшла. На якому поверсі вийшла Іра?
Задача 3. Якщо мале підприємство має на рахунку 5 000 грн, то будемо говорити, що воно має + 5 000 грн. Якщо ж підприємство заборгувало банку 5 000 грн, то будемо говорити, що воно має – 5 000 грн. Скільки грошей має мале підприємство, якщо воно:
А) має на рахунку 700 грн; 1 500 грн;
Б) заборгувало банку 750 грн; 3 000 грн?
Задача (на повторення). Екскурсантів можна посадити в човни або по 4 особи, або по 6 осіб. У кожному разі вільних місць не залишиться. Скільки було екскурсантів, якщо їх більше за 40, але менше від 50?
(1 votes, average: 5,00 out of 5)