1-й семестр
МЕХАНІКА
2. Динаміка
Урок 7/27
Тема. Сила тяжіння. Рух тіла під дією сили тяжіння
Мета уроку: дати учням уявлення про поняття сили тяжіння; ознайомити з природою цієї сили. Познайомити їх з рухом тіла під дією сили тяжіння
Тип уроку: вивчення нового матеріалу
План уроку
Контроль знань | 5 хв. | 1. Закон всесвітнього тяжіння. 2. Фізичний зміст гравітаційної сталої. 3. Межі застосовності закону всесвітнього тяжіння |
Демонстрації | 5 | 1. Падіння тіл на землю. 2. Центр ваги тіл. 3. Рух тіла, кинутого вертикально вгору і вниз. 4. Рух тіла, кинутого горизонтально. 5. Рух тіла, кинутого під кутом до горизонту |
Вивчення нового матеріалу | 25 хв. | 1. Сила тяжіння й центр ваги. 2. Прискорення вільного падіння. 3. Рух тіла по вертикалі. 4. Рух тіла, кинутого горизонтально. 5. Рух тіла, кинутого під кутом до горизонту |
Закріплення вивченого матеріалу | 10 хв. | 1. Тренуємося розв’язувати задачі. 2. Контрольні питання |
ВИВЧЕННЯ
1. Сила тяжіння й центр ваги
Камінь падає на Землю, тому що його притягує Земля. Камінь також притягує Землю. Сили взаємодії між каменем і Землею – це сили всесвітнього тяжіння. Для нас особливо важливе значення має сила притягання тіл до планети, на якій ми живемо, – до Землі. Тому сила тяжіння визначається як сила, з якою тіло притягується до Землі в певному місці. Тепер ми можемо додати, що це окремий випадок гравітаційних сил.
O Силу, з якою Земля притягує будь-яке тіло, називають силою тяжіння.
Під час вільного падіння всі тіла біля поверхні Землі рухаються з однаковим прискоренням, що називають прискоренням вільного падіння 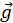 . Це прискорення зумовлене дією на тіло сили тяжіння
. Це прискорення зумовлене дією на тіло сили тяжіння 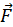 T.
T.
Отже, другий закон Ньютона для тіла, що вільно падає, має вигляд:
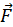 = m
= m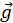 .
.
Таким чином,
O сила тяжіння, що діє на тіло, пропорційна масі цього тіла.
Сила тяжіння діє на всі тіла. Але до якої точки прикладена ця сила, якщо тіло не можна вважати матеріальною точкою? Найпростіше відповісти на це запитання за допомогою досліду.
Візьмемо тіло довільної форми, виготовлене з картону, і проколемо його голкою. Злегка погойдуючи фігуру, можна переконатися в тому, що вона перебуває в рівновазі. Вертикаль можна визначити за допомогою підвісу.
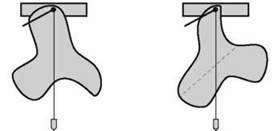
У точці підвісу на тіло діють сила тяжіння 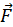 T і сила пружності нитки
T і сила пружності нитки 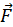 Пр. Під дією цих сил тіло перебуває в стані рівноваги. Тому, відповідно до другого закону Ньютона,
Пр. Під дією цих сил тіло перебуває в стані рівноваги. Тому, відповідно до другого закону Ньютона, 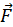 T +
T + 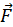 Np = 0. Звідси випливає, що
Np = 0. Звідси випливає, що 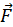 T = –
T = –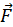 Пр, тобто сила тяжіння і сила пружності спрямовані протилежно й лінії їх дії знаходяться на одній прямій. Проведемо цю пряму (див. рис.). Повторимо дослід, прикріпивши голку за підвісом в іншій точці, і знайдемо нову лінію дії сили. Проведені лінії дії сили тяжіння перетинаються в одній точці. Ця точка і є центром ваги тіла.
Пр, тобто сила тяжіння і сила пружності спрямовані протилежно й лінії їх дії знаходяться на одній прямій. Проведемо цю пряму (див. рис.). Повторимо дослід, прикріпивши голку за підвісом в іншій точці, і знайдемо нову лінію дії сили. Проведені лінії дії сили тяжіння перетинаються в одній точці. Ця точка і є центром ваги тіла.
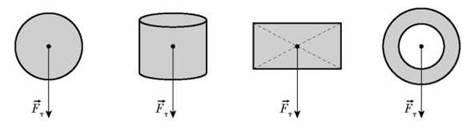
O Точку прикладання сили тяжіння, що діє на тіло, за будь-якого його положення в просторі називають центром ваги.
Для однорідного симетричного тіла центр ваги перебуває в центрі симетрії, при цьому центр ваги може не збігатися з жодною точкою тіла.
2. Прискорення вільного падіння
Розглядаючи Землю як однорідну кулю, розуміємо, що Земля притягує тіло масою яке знаходиться на її поверхні, із силою:  де М3 – маса Землі, R3 – радіус Землі. Ця сила надає тілам прискорення вільного падіння, що дорівнює:
де М3 – маса Землі, R3 – радіус Землі. Ця сила надає тілам прискорення вільного падіння, що дорівнює:
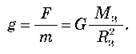
З отриманої формули видно, що прискорення вільного падіння визначається лише масою Землі та відстанню від центра Землі до тіла, тому прискорення вільного падіння є однаковим для всіх тіл незалежно від їхньої маси.
Оскільки земна куля трохи сплюснута біля полюсів (екваторіальний радіус Землі більший за полярний на 21 км), то прискорення вільного падіння збільшується залежно від переміщення: екватор – полюс. Однак сплюснутість Землі – не головна причина залежності прискорення вільного падіння від географічної широти місцевості.
Іншою істотною причиною є обертання Землі навколо своєї осі. Ці дві причини зумовлюють те, що прискорення вільного падіння на різних широтах відрізняються: на полюсах – gпол? 9,83 м/с2, на екваторі – geкв? 9,78 м/с2, а на широті 45° – g? 9,81 м/с2.
Крім того, прискорення вільного падіння в певній місцевості може відрізнятися через неоднорідність будови земної кори, наявність гір і западин, а також через різну густину порід, що залягають у надрах Землі. Зменшення прискорення вільного падіння часто свідчить про поклади таких корисних копалин, як торф, нафта, газ; збільшення – про поклади металевих руд.
Метод знаходження покладів корисних копалин за точним значенням прискорення вільного падіння називають гравіметричною розвідкою.
3. Рух тіла по вертикалі
Камінь, що падає зі скелі, і м’яч, кинутий вертикально вгору, рухаються по прямій. Розігнавшись на березі, людина стрибає у воду, при цьому траєкторія її тіла – половинка параболи. Снаряд, випущений з гармати під кутом до горизонту, також опише в просторі параболу. Траєкторія супутника Землі дуже близька до кола. Рух усіх цих тіл відбувається під дією сили тяжіння. Чому ж ці рухи настільки відрізняються один від одного? Очевидно, причина – різні початкові умови.
Якщо на тіло діє лише сила тяжіння, то, відповідно до другого закону Ньютона, 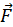 Т = m
Т = m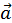 , або m
, або m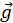 = m
= m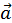 . Це означає, що під дією сили тяжіння тіло рухається рівноприскорено з прискоренням g (а = g). При цьому рівняння залежності швидкості від часу має вигляд:
. Це означає, що під дією сили тяжіння тіло рухається рівноприскорено з прискоренням g (а = g). При цьому рівняння залежності швидкості від часу має вигляд: 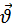 =
= 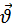 0 +
0 + 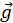 T.
T.
Це рівняння показує, що швидкість руху тіла перебуває у площині, утвореній векторами 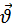 0 і
0 і 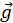 , тому для опису таких рухів достатньо двовимірної системи координат.
, тому для опису таких рухів достатньо двовимірної системи координат.
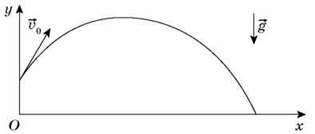
Розглянемо рух тіла по вертикалі: тіло кинули вертикально вгору (рис. а), і тіло падає вертикально вниз (рис. б).
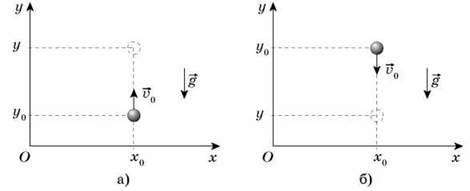
У цьому випадку траєкторією руху тіла буде відрізок прямої, оскільки руху вздовж осі Ох не відбувається (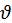 0х = 0, х = х0).
0х = 0, х = х0).
Оскільки під час руху вгору 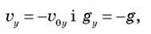 То рівняння руху матимуть такий вигляд:
То рівняння руху матимуть такий вигляд:
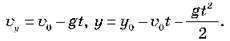
Аналогічно, під час руху тіла, кинутого вниз, 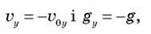 Рівняння матимуть вигляд:
Рівняння матимуть вигляд:
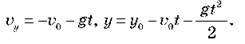
4. Рух тіла, кинутого горизонтально
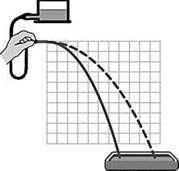
Проведемо кілька дослідів зі струменем води, що витікає з наконечника гумової трубки, з’єднаної з водопровідним краном. Струмінь показує траєкторію руху частинок води, випущених з наконечника гумової трубки, розташованого горизонтально. Виконуючи кілька дослідів з різною швидкістю витікання води, переконуємося в тому, що траєкторія руху тіла, кинутого горизонтально, – парабола, вершина якої знаходиться в початковій точці руху.
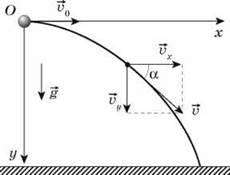
Розмістимо початок координат у крапці, з якої кинуто тіло (див. рис).
Хоча рух тіла буде криволінійним, однак залежність швидкості тіла від часу, як і раніше, описується формулою:  =
= 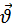 0 +
0 + 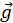 T. Тіло, що рухається, ніби бере участь одночасно у двох уже знайомих нам рухах:
T. Тіло, що рухається, ніби бере участь одночасно у двох уже знайомих нам рухах:
А) по горизонталі – рівномірний прямолінійний рух:
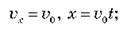
Б) по вертикалі – прискорений рух (без початкової швидкості):
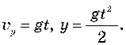
Підставивши в останню формулу вираз для часу руху 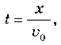 дістаємо:
дістаємо: 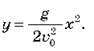
O Отже, тіло, кинуте горизонтально, рухається по параболі, вершина якої знаходиться в початковій точці руху.
А час польоту і дальність польоту можна обчислити за формулами:
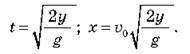
Слід звернути увагу учнів на те, що час руху тіла, кинутого горизонтально з певної висоти, і час руху тіла, яке вільно падає з цієї ж висоти, однаковий. Цей висновок можна проілюструвати дослідом на приладі для порівняння часу падіння двох кульок.
Швидкість тіла в будь-якій точці траєкторії можна обчислити за формулою:
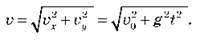
Ця швидкість буде спрямована по дотичній до траєкторії, а напрям вектора швидкості визначається кутом, який він утворює з горизонтальною віссю:
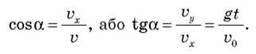
5. Рух тіла, кинутого під кутом до горизонту
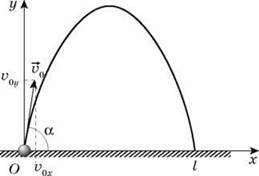
Проведемо кілька дослідів зі струменем води, що витікає з наконечника гумової трубки, з’єднаної з водопровідним краном. Струмінь показує траєкторію руху частинок води, випущених з наконечника гумової трубки під кутом до горизонту. Форма струменя – парабола. Отже, траєкторією руху тіла й у цьому випадку буде парабола. Однак тепер вершина параболи – точка, що відповідає підйому тіла на максимальну висоту.
Нехай тіло кинули зі швидкістю 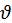 0 під кутом
0 під кутом 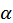 до горизонту. З’єднаємо початок координат з початковим положенням тіла, спрямуємо вісь Оу вертикально вгору, а вісь Ох – горизонтально (див. рис). У обраній системі координат:
до горизонту. З’єднаємо початок координат з початковим положенням тіла, спрямуємо вісь Оу вертикально вгору, а вісь Ох – горизонтально (див. рис). У обраній системі координат:
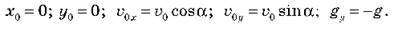
Оскільки й у цьому випадку 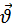 =
= 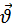 0 +
0 + 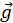 T, дістаємо:
T, дістаємо:
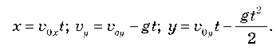
Коли тіло перебуває на максимальній висоті, його швидкість спрямована горизонтально, тобто проекція швидкості на вісь Оу дорівнює нулю (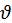 Y = О). Оскільки
Y = О). Оскільки 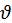 Y =
Y = 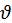 0y – gt, для часу підйому тіла на максимальну висоту отримуємо:
0y – gt, для часу підйому тіла на максимальну висоту отримуємо:
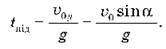
Знаючи час підйому тіла, можна розрахувати висоту, на яку воно підніметься: для цього достатньо підставити у формулу 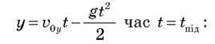
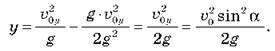
Час польоту тіла складається з часу підйому й часу наступного падіння, а оскільки час підйому дорівнює часу падіння, то час польоту вдвічі більший за час підйому:
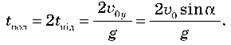
Оскільки x =  0xtпoл, можна обчислити дальність польоту тіла, кинутого під кутом до горизонту:
0xtпoл, можна обчислити дальність польоту тіла, кинутого під кутом до горизонту:
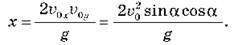
Скориставшись перетворенням 2sin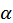 Cos
Cos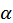 = sin2
= sin2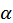 , дістаємо:
, дістаємо:
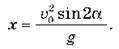
З цього виразу випливає, що з таким значенням початкової швидкості 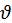 0, максимальна дальність польоту досягається за максимального значення sin2
0, максимальна дальність польоту досягається за максимального значення sin2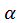 . Найбільше значення синуса дорівнює 1 (якщо кут – 90°). Отже, 2
. Найбільше значення синуса дорівнює 1 (якщо кут – 90°). Отже, 2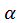 = 90°, звідки
= 90°, звідки 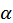 = 45°. Отже, максимальна дальність польоту досягається, якщо кут
= 45°. Отже, максимальна дальність польоту досягається, якщо кут 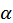 = 45° і дорівнює:
= 45° і дорівнює:
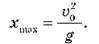
Питання до учнів під час вивчення нового матеріалу
1. На підставі якого закону можна стверджувати, що сила тяжіння пропорційна масі тіла?
2. Як залежить прискорення вільного падіння від висоти над поверхнею Землі?
3. З яким прискоренням рухається тіло, кинуте горизонтально?
4. Чи залежить час польоту тіла, кинутого горизонтально, від значення величини початкової швидкості?
5. Чи можна рух тіла, кинутого під кутом до горизонту, вважати рівноприскореним?
6. Що спільного в русі тіл, кинутих вертикально вгору і під кутом до горизонту?
ЗАКРІПЛЕННЯ ВИВЧЕНОГО МАТЕРІАЛУ
1). Тренуємося розв’язувати задачі
1. Обчисліть масу Землі, якщо відомо, що її радіус дорівнює 6400 км.
2. Обчисліть прискорення вільного падіння на висоті, що дорівнює радіусу Землі.
3. З якою швидкістю треба кинути тіло горизонтально з певної висоти, щоб дальність польоту дорівнювала висоті, з якої кинуто тіло?
4. Камінь, кинутий горизонтально з даху будинку зі швидкістю 15 м/с, упав на землю під кутом 60° до горизонту. Якою є висота будинку?
5. Камінь, кинутий під кутом 30° до горизонту, двічі побував на одній висоті: за 3 с і за 5 с після початку руху. Обчисліть початкову швидкість кидання й максимальну висоту підйому.
2). Контрольні запитання
1. Чому зі збільшенням висоти над поверхнею Землі прискорення вільного падіння зменшується?
2. Чи може тіло під дією сили тяжіння рухатися по колу? Обгрунтуйте свою відповідь.
3. Що спільного в русі тіл, кинутих вертикально вгору і під кутом до горизонту?
4. Як зміниться час і дальність польоту тіла, кинутого горизонтально з певної висоти, якщо швидкість кидання збільшити вдвічі?
5. Тіло, кинуте під кутом 30° до горизонту, впало в певну точку на поверхні землі. Під яким іншим кутом треба кинути друге тіло з тією ж початковою швидкістю, щоб воно впало в ту ж точку, що і перше?
Що ми дізналися на уроці
– Силу, з якою Земля притягує будь-яке тіло, називають силою тяжіння.
– Сила тяжіння, що діє на тіло, пропорційна масі цього тіла.
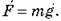
– Точку прикладання сили тяжіння, що діє на тіло, за будь-якого його положення в просторі називають центром ваги.
– Прискорення вільного падіння дорівнює:
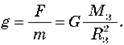
– Якщо на тіло діє лише сила тяжіння, то рівняння залежності швидкості тіла від часу має вигляд:
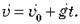
– Тіло, кинуте горизонтально, рухається по параболі, вершина якої знаходиться в початковій точці руху.
– Час польоту і дальність польоту тіла, кинутого горизонтально, обчислюються за формулами:
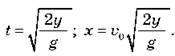
– Під час руху тіла, кинутого під кутом до горизонту:
А) висота підйому тіла – 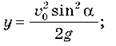
Б) дальність польоту тіла – 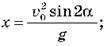
В) максимальна дальність польоту 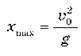 Досягається, якщо кут
Досягається, якщо кут 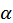 = 45°.
= 45°.
Домашнє завдання
1. П.: §§ 21, 22.
2. 36.:
Р1) – 7.8; 7.21; 7.28, 8.6; 8.7;
Р2) – 7.54; 7.55; 7.56. 8.13, 8.14;
Р3) – 7.75; 7.81; 8.34; 8.39, 8.40.
