УРОК № 58
Тема. Куля. Площа поверхні та об’єм кулі
Мета уроку: повторення, приведення в систему й розширення відомостей про кулю (сферу), площу поверхні та об’єм кулі; формування вмінь учнів знаходити площі поверхонь і об’єми куль.
Тип уроку: комбінований.
Наочність і обладнання: таблиця “Початкові відомості стереометрії” [13]; моделі куль.
Вимоги до рівня підготовки учнів: пояснюють, що таке куля та її елементи; зображують і знаходять на рисунку кулю; записують й пояснюють формули площі поверхні та об’єму
Хід уроку
І. Перевірка домашнього завдання
Перевірити наявність виконаного домашнього завдання та відповісти на запитання, які виникли в учнів при розв’язуванні задачі.
Розв’язання
Нехай SA = 15 см, SO = 9 см (рис. 277). Із трикутника SAO маємо: АО = 
= 
= 12 (см).
Sкон = Sосн + Sбічн = n • AO2 + n • AO • AS = n • 122 + n • 12 • 15 = 144n + 180n = 324n(см2). V =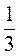 
NАО2 • SO = 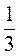N • 144 • 9 = 432(см3).
Відповідь. 324n см2, 432n см3.
Фронтальна бесіда
Конус утворено в результаті обертання прямокутного трикутника навколо катета (рис. 278), який дорівнює а й утворює кут? з гіпотенузою. Визначте, які з наведених тверджень є правильними, а які – неправильними.
А) Твірна конуса дорівнює acos?.
Б) Радіус конуса дорівнює 
.
В) Площа бічної поверхні конуса дорівнює nа2
.
Г) Об’єм конуса дорівнює 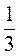Na3 tg2?.
II. Поетапне сприймання й усвідомлення нового матеріалу
Куля та її елементи
Кулею називається тіло, утворене обертанням круга навколо діаметра (рис. 279).
Сферою називається фігура, утворена обертанням кола навколо діаметра. (Демонструються моделі куль (сфер).)
Можна дати й інші означення сфери і кулі.
Сферою називається поверхня, яка складається з усіх точок простору, що розташовані на даній відстані (яка називається радіусом) від даної точки (яка називається центром).
Відрізок, який сполучає центр сфери з точкою сфери, називається радіусом сфери. Відрізок, який сполучає дві точки сфери і проходить через центр сфери, називається діаметром сфери. На рис. 279 точка О – центр сфери, ОА, ОВ – радіуси сфери, АВ – діаметр сфери.
Кулею називається тіло, що складається з усіх точок простору, які розташовані від даної точки на відстані, не більшій за дану. Ця точка називається центром кулі, а дана відстань – радіусом кулі.
Площина, яка проходить через центр кулі (сфери), називається діаметральною площиною.
Переріз кулі (сфери) діаметральною площиною називаються великим кругом (великим колом).
Завдання класу
1. Наведіть приклади побутових предметів, що мають форму кулі (сфери). 2. Радіус кулі 
см. Укажіть, усередині чи поза кулею розміщена точка А, якщо вона віддалена:
А) від центра кулі на 1 см;
Б) від центра кулі на 1,5 см.
Площа поверхні й об’єм кулі
Строгі міркування (ми їх не. наводимо) показують, що площа сфери в 4 рази більша від площі великого круга.
Отже, якщо радіус сфери – R (рис. 280), то її площа: S = 4nR2.
Об’єм кулі обчислюється за формулою V = 
NR3.
Розв’язування задач
1. Знайдіть площу поверхні кулі, діаметр якої 10 см. 2. Площа великого круга кулі дорівнює 20? см2. Знайдіть площу поверхні кулі. 3. Радіус кулі дорівнює 9 см. Знайдіть об’єм кулі. 4. Знайдіть об’єм кулі, діаметр якої дорівнює 12 см. 5. Знайдіть площу великого круга і довжину великого кола, якщо радіус кулі дорівнює 2 см.
Наводимо зразок конспекту учнів (табл. 14).
Таблиця 14
Куля (сфера) | |
| Куля (сфера) – фігура, утворена обертанням круга (кола) навколо його діаметра. О – центр кулі (сфери); ОА, ОВ – радіуси; АВ – діаметр |
| Площа поверхні кулі (площа сфери) S = 4nR2 Об’єм кулі V = |
III. Закріплення й осмислення нового матеріалу
Розв’язування задач
1. Об’єми двох куль відносяться як 27 : 64. Як відносяться площі їхніх поверхонь? 2. Площі поверхонь двох куль відносяться як 9 : 16. Як відносяться об’єми куль? 3. Припустимо, що Земля має форму кулі радіусом приблизно 6400 км, тоді суша становить 30% площі всієї поверхні планети. Знайдіть площу суші. (Відповідь. 154 337 280 км2.) 4. Дві чавунні кулі діаметрами 8 см і 12 см переплавили в одну кулю. Знайдіть радіус цієї кулі.
IV. Самостійна робота
Самостійну роботу навчального характеру можна провести за посібником [14], тест 19 “Тіла обертання”.
V. Домашнє завдання
1. Вивчити формули площі поверхні та об’єму кулі. 2. Підготуватися до тематичної контрольної роботи. 3. Розв’язати задачу. 4. Площа сфери дорівнює 400? см2. Знайдіть її об’єм.
VI. Підбиття підсумків уроку
Запитання до класу
1. Дайте означення кулі (сфери). 2. Що таке великий круг (велике коло)? 3. Чому дорівнює площа сфери? 4. Чому дорівнює об’єм кулі?
(2 votes, average: 3,00 out of 5)