Геометрія
Об’єми тіл
Об’єм кулі
На рисунку зображено кулю, кульовий сегмент і кульовий сектор.
Об’єм кулі:
, де R – радіус кулі.
Об’єм кульового сегмента:
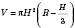, де H – висота кульового сегмента,
R – радіус кулі.
Об’єм кульового сектора:
, де R – радіус кулі, H – висота відповідного кульового сегмента.
Іноді треба знайти об’єм або площину поверхні тіла обертання. Щоб правильно
1. Відрізок обертається навколо осі, на якій лежить один із його кінців (див. рисунок нижче зліва).
l – пряма. Проведемо
. Отже, точка 
є проекцією B на пряму l. Відрізок AB, обертаючись навколо осі, утворює бічну поверхню конуса з вершиною A, висотою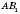 
і радіусом основи 
.2. Відрізок обертається навколо осі, якій він є паралельним (див.
Спроектуємо точки A і B на вісь l.
Дістанемо точки
і 
.Очевидно, що при обертанні AB навколо l дістанемо бічну поверхню прямого кругового циліндра, у якого AB – твірна, вісь – пряма l, радіус основи –
.
3. Відрізок обертається навколо осі (див. рисунок), він не є їй паралельним і лежить з нею в одній площині, не перетинаючи осі.
Нехай точки
і 
– проекції точок A і B на вісь l відповідно.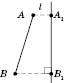
При обертанні AB навколо l дістанемо бічну поверхню зрізаного конуса, у якого AB – твірна,
– центр верхньої основи, 
– центр нижньої основи, 
– радіус верхньої основи, 
– радіус нижньої основи.Якщо навколо осі обертається який-небудь многокутник, треба спроектувати на вісь обертання всі вершини многокутника й розібрати, які фігури утворюють усі його сторони при обертанні.
(1 votes, average: 5,00 out of 5)