УРОК № 18
Тема. Формули радіусів вписаних і описаних кіл правильних многокутників
Мета уроку: Виведення формул для радіусів вписаних і описаних кіл правильного многокутника. Формування вмінь застосовувати виведені формули до розв’язування задач.
Тип уроку: комбінований.
Наочність і обладнання: табл. 5, 6.
Вимоги до рівня підготовки учнів: записують і пояснюють формули радіусів вписаного та описаного кіл правильного многокутника; радіусів вписаного й описаного кіл правильного трикутника, чотирикутника (квадрата),
Хід уроку
І. Перевірка домашнього завдання
Перевірити наявність виконаних домашніх завдань та відповісти на запитання, які виникли в учнів під час виконання домашніх завдань.
Задача 1. Розв’язання
Оскільки 
= 150°, то 180 • (n – 2) = 150n; 180n – 360 = 150n; 30n = 360; n = 12.
Відповідь. 12 сторін.
Задача 2. Розв’язання
Оскільки 
= 24°, то 360 = 24n; n = 15.
Відповідь. 15 сторін.
Задача 3. Доведення
Нехай А1А2…Аn – даний правильний n-кутник (рис. 74), точка О – його центр. В1, В2, …, Вn – середини сторін А1А2,
Тоді ОВ1 = ОВ2 = … = ОВn – як радіуси вписаного кола в многокутник А1А2…Аn і 
В1ОВ2 = В2ОВ3 = … = BnOB1 = 2B1OA2. Рівнобедрені трикутники В1ОВ2, В2ОВ3,…, ВnОВ1 рівні за двома сторонами і кутом між ними. Із рівності трикутників маємо: В1В2 = В2В3 = … = ВnВ1і B1B2B3= B2B3B4 = …= BnB1B2 = 2OB1B2. Отже, n-кутник В1В2…Вn правильний.
Математичний диктант
Дано правильний п-кутник.
Варіант 1 (n = 4), варіант 2 (n = 6).
Знайдіть:
А) суму кутів многокутника;
Б) внутрішній кут многокутника;
В) зовнішній кут многокутника;
Г) центральний кут многокутника;
Д) сторону многокутника, якщо його периметр дорівнює 24 см;
Є) апофему многокутника, якщо його сторона дорівнює 20 см.
Відповіді
Варіант 1. а) 360°; б) 90°; в) 90°; г) 90°; д) 6 см; є) 10 см.
Варіант 2. а) 720°; б) 120°; в) 60°; г) 60°; д) 4 см; є) 10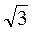
см.
II. Сприймання й усвідомлення нового матеріалу
Виведення формул радіусів вписаного і описаного кіл правильного многокутника
Нехай задано сторону an правильного n-кутника (рис. 75), знайдемо радіус R описаного кола і радіус r вписаного кола.
Розглянемо трикутник АОВ, у якому АВ = an, АОВ = як центральний кут правильного n-кутника. Проведемо висоту ОС цього трикутника, тоді АОС = 
= 
= 
.
Із трикутника АОС знаходимо:
R = AO = 
= 
; r = OC = 
= 
.
Отже, 
, 
.
Виведення формул радіусів вписаного і описаного кіл правильного трикутника, чотирикутника, шестикутника.
Виразимо радіуси описаного та вписаного кіл через сторону правильного трикутника, чотирикутника і шестикутника.
Для правильного трикутника (рис. 76):
;
.
Для правильного чотирикутника (рис. 77):
;
.
Для правильного шестикутника (рис. 78):
;
.
Результати наших досліджень оформимо у вигляді табл. 5.
Таблиця 5
N R, r | N – довільне, | N = 3 | N = 4 | N = 6 |
R |
|
|
| A6 |
R |
|
|
|
|
Виконання вправ
1) Сторона квадрата дорівнює 20 см. Знайдіть радіуси вписаного й описаного кіл. 2) Сторона правильного трикутника дорівнює 15 см. Знайдіть радіуси вписаного й описаного кіл. 3) Сторона правильного шестикутника дорівнює 12 см. Знайдіть радіуси вписаного й описаного кіл. 4) У правильного трикутника радіус вписаного кола вдвічі менший за радіус описаного кола. Доведіть це.
Доведення
Оскільки R = 
, а r = 
, то R : r = • 
= 2, що і треба було довести.
5) Радіус кола, описаного навколо правильного трикутника, дорівнює 2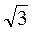 см. Знайдіть сторону трикутника і радіус кола, вписаного в цей трикутник. 6) Радіус кола, вписаного в правильний чотирикутник, дорівнює 
см. Знайдіть сторону чотирикутника і радіус кола, описаного навколо цього чотирикутника. 7) Радіус кола, описаного навколо правильного шестикутника, дорівнює 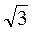см. Знайдіть сторону цього шестикутника та діаметр кола, вписаного в цей шестикутник.
Колективне розв’язування задачі
Виразіть сторону аn правильного n-кутника через радіус R описаного навколо нього і радіус r вписаного в нього кола. Обчисліть аn, якщо n = 3, 4, 6.
Результати розв’язування задачі можна оформити у вигляді табл. 6.
Таблиця 6
R, r An | R | Г |
An | 2R sin | 2r tg |
A3 | R | 2r |
A4 | R | 2r |
А6 | R |
|
rIII. Закріплення й осмислення нового матеріалу
Розв’язування задач
1. Хорда, яка перпендикулярна до радіуса й проходить через його середину, дорівнює стороні правильного вписаного трикутника. Доведіть це.
Доведення
Нехай AB 
OD, DC = CO (рис. 79). У прямокутному трикутнику ВОС катет CO дорівнює половині гіпотенузи ВО. Нехай
BO = R, тоді СО = 
, АВ = 2 • ВС = 2 
= 
= R.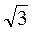
Отже, довжина хорди дорівнює стороні правильного трикутника.
2. Сторона правильного трикутника, вписаного в коло, дорівнює а. Знайдіть сторону правильного шестикутника:
А) вписаного в це коло;
Б) описаного навколо цього кола.
Розв’язання
Сторона правильного трикутника дорівнює а, отже, радіус описаного кола R = 
.
А) Радіус кола, описаного навколо трикутника, дорівнює радіусу кола, описаного навколо шестикутника, і тому сторона цього шестикутника b = R = .
Б) Радіус кола, описаного навколо трикутника, є апофемою правильного шестикутника, і тому сторона цього шестикутника b = 
= 
= 
.
Відповідь: а) b = ; б) b = .
IV. Домашнє завдання
1. Вивчити формули радіусів вписаного і описаного кіл правильного n-кутника. 2. Розв’язати задачі. 1) Сторона правильного вписаного в коло трикутника дорівнює а. Знайдіть сторону квадрата, вписаного в це коло. 2) У коло радіуса 4 см вписано правильний трикутник, на стороні якого побудовано квадрат. Знайдіть радіус кола, описаного навколо квадрата.
V. Підбиття підсумків уроку
Запитання до класу
1. Запишіть, як виражаються радіуси вписаного й описаного кіл правильного n-кутника через його сторону. 2. Чому дорівнюють радіуси вписаних і описаних кіл для правильного трикутника, чотирикутника, шестикутника?
(2 votes, average: 2,50 out of 5)