605.
А) 10! = 2×3×4×5×6×7×8×9×10 = 3 628 800;
Б) 13! = 10!×1×12×13 = 6 227 020 800;
В) 20! = 13!×4×15×16×17×18×19×20;
Г) 25! = 20!×21×22×23×24×25.
606.
А) n!(n + 1) = (n + 1)!;
Б) n(n – 1)! = nі;


607.
Печиво можна купити 3 способами, цукерки – 10 способами.
Усього 3 + 10 = 13 способів (правило суми).
608.
Чотирьох дітей на лавці можна посадити 4! = 24 способами.
609.
Вибір для підйому – 4 способи (4 стежки), а вибір для спуску – 3 способи
(стежки
610.
Усього 3×2 = 6 наборів.

611.
Чергу можна утворити 5! = 120 способами.
612.
1. 3! = 6 способів.
2. 4! = 24 способи.
613.
Дівчина може нанизати 8! способами 8 різних намистин.
8! = 2×З×4×5×6×7×8 = 40 320.
614.
Якщо цифри не повторюються, то 5×4×3 = 60 способів.
615.
А) 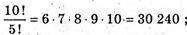
Б) 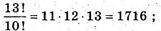
В) 
Г) 
616.
А) 
Б) 
В) 
617.

А) n = 3, 
Б) n = 4, 
В) n = 10, 
618.
А) n! = (n – 1)!×8,  n = 8;
n = 8;
Б) (n + 2)! = 132n!, 
(n+ 1)(n + 2) = 132, n2 + 3n – 130 = 0, n = 10.
619.
Кожний з восьми друзів зіграв 7 партій.
Всього  партій.
партій.
620.
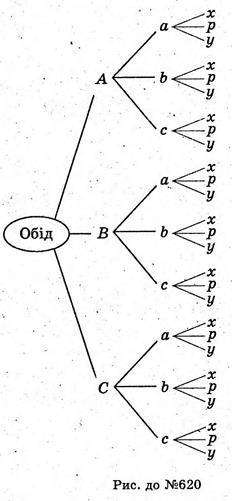
Різних наборів із трьох страв можна одержати 8×3×3 = 27 способами.
621.
Коли рух до моря і з моря відбувається:
А) одним шляхом, то 7 способами;
Б) різними шляхами, то 7×6 = 42 способи;
В) одним із двох попередніх способів
7 + 42 = 49 способів або 7×7 = 49.
622.

Різних “кортежів” можна створити 4×3×x2 = 24 способами.
623.
Непарне число закінчується непарною цифрою (1, 3, 5),
Тому її можна вибрати трьома способами.
Перша цифра не може бути 0, тому її можна вибрати чотирма способами.
Друга цифра може бути будь-якою, тоді її можна вибрати чотирма способами,
А третю цифру – трьома способами. Усього: З×4×4×хЗ = 144 способи.
624.
Щоб уроки алгебри і геометрії стояли поруч, необхідно,
Щоб виконувалась одна з умов, це: алгебра і геометрія – (1, 2) уроки;
(2, 3) уроки; (3, 4) уроки, (4, 5) уроки або (5, 6) уроки.
Всього 5 способів. Інші 4 уроки можна розподілити 4! способами.
Всього: 5×2×4! способів (алгебру і геометрію можна міняти місцями).
Відповідь: 240 способів розкладу, щоб алгебра і геометрія стояли поруч.
Узагальнення: нехай уроків n і 2 заданих уроки стоять поруч,
Тоді кількість способів дорівнює 2(n – 1)!.
У даному випадку n = 6 і число способів 2×5! = 240.
625.
Нехай фізика стоїть на 1-му уроці, тоді астрономію можна поставити на З, 4, 5, 6, 7 урок. Усього 5 способів, крім того, фізику і астрономію можна міняти місцями.
Інші 5 уроків розподіляються 5! способами, тобто 5×2×5! способів. Якщо фізика стоїть на 2-му уроці, то астрономію можна поставити на 4, 5, 6, 7-й урок.
Це дає 4×2×5! способів. Якщо фізика на 3-му уроці, то астрономія на 5, 6, 7-му уроці (3×2×5! способів). Фізика на 4-му уроці, астрономія на 6, 7-му уроці (2×2×5! способів). Фізика на 5-му уроці, астрономія на 7-му уроці (1×2×5! способів).
Усього
×2×5!+4×2×5!+3×2×5!+2×2×5!+1×2×5!=2×5!(5+4+3+2+1)=30×5!=5×6!=3600 способів.
626.

{a, b, с, d,}
Із чотирьох елементів можна побудувати чотири трьохелементні підмножини:
{a, b, с}, {a, b, d}, {а, с, d}, {b, с, d}.
Упорядкованих підмножин буде 4×3! = 4! = 24.
627.

Із пункту А в пункт С веде декілька шляхів (див. рис.).
Скількома способами можна попасти з А в С?
(4×3 + 2×3 = 18)
Подарунковий набір складається з печива двох сортів;
Цукерок: карамелі і шоколаду і зефіру: білого і рожевого.
Скільки різних наборів можна скласти?
(3×2 = 6)
