Розділ 2. ФУНКЦІЇ
& 21. Лінійна функція, її графік та властивості
Приклад 1. Маса одного цвяха 4 г, а маса порожнього ящика – 600 г. Залежність між масою т (у г) ящика із цвяхами і кількістю цвяхів у ньому, що дорівнює х (х – натуральне число), можна задати формулою:
M = 4x + 600.
Приклад 2. Щомісячна зарплата продавця становить 1500 грн та ще премія в розмірі 1 % від вартості реалізованого товару. Залежність між зарплатою y (y грн) і вартістю х (у грн) реалізованого товару можна задати формулою: у = 0,01х + 1500, де х > 0.
В обох прикладах функції
Числа k і l називають коефіцієнтами лінійної функції.
З’ясуємо, як виглядає графік лінійної функції. У формулі у = kx + l незалежній змінній х можна надавати будь-яких значень, тому область визначення лінійної функції складається з усіх чисел.
Приклад 3. Побудувати графік функції у = 0,25 х – 1.
Р о з в ‘ я з а н н я. Функція є лінійною. Складемо для неї таблицю кількох значень незалежної змінної х та відповідних їй значень функції у:
Х | -8 | -4 | 0 | 4 | 8 |
У | -3 | -2 | -1 | 0 | 1 |
Позначимо
Мал. 18
Оскільки пряма однозначно задається двома своїми точками, для побудови прямої, яка є графіком лінійної функції, достатньо знайти координати двох точок графіка, позначити ці точки на координатній площині і провести через них пряму.
Приклад 4. Побудувати графік функції у = -2х + 3.
Р о з в ‘ я з а н н я. Складемо таблицю для двох довільних значень аргументу.
Позначимо па координатній площині одержані точки та проведемо через них пряму. Маємо графік функції у = -2х + 3 (малюнок 19).
Х | 0 | 4 |
У | 3 | -5 |
Якщо коефіцієнти лінійної функції є дробовими, то для знаходження двох точок її графіка доцільно підбирати такі цілі значення аргументу, щоб відповідні їм значення функції також виходили цілими.
Наприклад, для функції у = 
Х – 
зручно взяти х = -1 та х = 5, тоді для побудови її графіка отримаємо точки (-1; -1) та (5; 1).
Якщо k = 0, формула у = kx + l матиме вигляд у = 0х + l, тобто у = l. Лінійна функція, яку задано формулою у = l, набуває одних і тих самих значень при будь-яких значеннях х.
Мал. 19
Мал. 20
Приклад 5. Побудувати графік функції у = -3.
Р о з в ‘ я з а н н я. Будь-якому значенню х відповідає одне й те саме значення у, що дорівнює -3. Графіком функції є пряма, яка проходить через точки вигляду (х -3), де х – будь-яке число. Виберемо будь-які дві з них, наприклад (-5; -3) і (2; -3), та проведемо через них пряму (мал. 20). Ця пряма і є графіком функції у = -3. Вона паралельна осі х.
Отже,
Щоб побудувати графік функції у = l, достатньо позначити на осі у точку з координатами (0; l) та провести через неї пряму, паралельну осі х.
Якщо l = 0, k ≠ 0, формула у = kx +l набуває вигляду у = kx.
Оскільки пряма пропорційність є окремим випадком лінійної функції, і до того ж при х = 0 значення у також дорівнює 0, то
На мал. 21 зображено графіки функцій у = – х; у = 2х; у = 0,2x. Узагальнимо властивості лінійної функції у = kx + l.
Мал. 21
Однією з важливих властивостей функції є існування точок перетину її графіка з осями координат.
Якщо на координатній площині графік функції вже зображено, то такі точки можна знайти безпосередньо з графіка. Наприклад, на малюнку 18 точкою перетину графіка функції у = 0,25х – 1 з віссю абсцис є точка (4; 0), а з віссю ординат – точка (0; -1). У такому випадку кажуть, що точки перетину знайдено графічно. Але графічний спосіб не завжди дає можливість визначити точні значення координат таких точок. Наприклад, на малюнку 19 визначити абсцису точки перетину графіка функції у = 2х + 3 з віссю абсцис можна лише наближено, наприклад х ≈ 1,5.
Отже, за допомогою графіка функції знайти точні значення абсциси точки перетину з віссю абсцис або ординати точки перетину з віссю ординат не завжди можливо.
Для багатьох функцій координати точок перетину графіка з осями координат можливо знайти, не виконуючи побудови графіка, зокрема, якщо функцію задано формулою. У такому випадку кажуть, що координати точок перетину знайдено аналітично, причому їх значення будуть точними, а не наближеними.
Приклад 6. Не виконуючи побудови, знайдіть координати точок перетину графіка функції у = 2х – 6 з осями координат.
Р о з в ‘ я з а н н я. Точка перетину графіка з віссю абсцис належить цій осі, отже, її ордината має дорівнювати нулю. Тому для пошуку точки (або точок) перетину графіка функції з віссю абсцис достатньо у формулу, якою задано функцію, підставити значення у = 0 і розв’язати одержане рівняння.
Підставимо 0 замість у в рівняння у = 2х – 6. Одержимо рівняння 2х – 6 = 0. Звідки х = 3. Отже, (3; 0) – точка перетину графіка функції з віссю абсцис.
Точка перетину графіка з віссю ординат належить цій осі, отже, абсциса такої точки має дорівнювати нулю. Тому для знаходження точки перетину графіка функції з віссю ординат достатньо у формулу, якою задано функцію, підставити значення х = 0 та виконати обчислення.
Підставимо 0 замість х в рівняння у = 2х – 6. Одержимо у = 2 ∙ 0 – 6, тобто, у = -6. Отже, (0; -6) – точка перетину графіка функції у = 2х – 6 з віссю ординат.
В і д п о в і д ь: (3; 0); (0; -6).
Зауважимо, що існують функції, графіки яких можуть не перетинати осі координат або хоча б одну з них.
Сформулюйте означення лінійної функції. Що є графіком лінійної функції? Як його побудувати? Як побудувати графік функції у – l, де l число? Яку функцію називають прямою пропорційністю? Які властивості має лілійна функція? Як знайти координати точок перетину графіка функції з осями координат?
769. (Усно) Чи є лінійною функція:
1) у = 2х – 5;
2) у = 2х – 5х2;
3) у = 8;
4) у = 
;
5) у = 
+ 3;
6) у = х – 1 – х5?
770. Які з даних функцій є лінійними:
1) у = 3х2 – 4;
2) у = 3х – 4;
3) у = 
;
4) у = – 2;
5) у = -8;
6) у = 5х – х3?
771. (Усно) Які з функцій задають пряму пропорційність:
1)у = 5х;
2) у = ;
3) у = х + 5;
4) у = 5;
5 )у = –
;
6)y = ?
772. Чи є прямою пропорційністю функція, яку задано формулою:
1) у = -4х;
2) у = -4х + 2;
3) у = – 
;
4) у = -4;
5)у = 
;
6)у = –?
773. (Усно) Назвіть коефіцієнти k і l у кожній з даних формул лінійних функцій:
1) у = -0,8x + 7;
2) у = 6 – х;
5) у = 
;
3) у = 2,4x;
4) у = -15;
6) у = 0.
774. Ширина прямокутника дорівнює x см, а довжина на см більша за ширину. Задайте формулою залежність:
1) периметра прямокутника від його ширини;
2) залежність площі прямокутника від його ширини.
Яка із цих залежностей є лінійною функцією?
775. Учень купив щоденник за 5 грн і кілька зошитів по 2 грн. Задайте формулою залежність вартості покупки у (у гривнях)
Від кількості придбаних зошитів х. Чи є ця залежність лілійною функцією? Якою є область визначення цієї функції?
776. Учень мав 30 грн. За ці кошти він придбав х олівців по 1,5 грн кожен, після чого в нього залишилося у грн. Задайте формулою залежність у від х. Чи є ця залежність лінійною функцією?
777. Лінійнy функцію задано формулою у = 0,5х + 3. Знайдіть:
1) значення у, якщо х = -12; 0; 18;
2) при якому значенні х значення у дорівнює -4; 8; 2,5.
778. Дано лінійну функцію у = -2х + 3. Знайдіть значення:
1) у, якщо х = 1,5; -4; -6,5;
2) х, при якому у = 5; 0; -8.
779. Використовуючи графік функції на малюнку 22, заповніть таблицю:
Мал. 22
Х | -2 | 0 | 1 | 3 |
У | -5 | -1 | 5 |
780. Використовуючи графік функції на малюнку 23, заповніть у зошиті таблицю:
Х | 6 | -2 | 2 |
У | -3 | -1 | 3 |
Мал. 23
781. Запишіть координати будь-яких двох точок, що належать графіку функції у = 5х – 2.
782. Заповніть у зошиті таблицю та побудуйте графік лінійної функції:
1) у = – х + 2;
Х | 0 | 4 |
У |
2) у – 2х – 3.
Х |
У |
783. Заповніть таблицю та побудуйте графік лінійної функції:
1) у = х – 3;
Х | 0 | 3 |
У |
2) у = -3х + 1.
Х |
У |
784. Побудуйте графік лінійної функції:
1) у = х + 2;
2) у = -3х + 4;
3) у = 0,5х – 3;
4) у = Х – 1;
5) у = -1;
6) у = – х + 4,5.
785. Побудуйте графік лінійної функції:
1) у = х – 1;
2) у = -2х + 5;
3) у = -0,5х + 3;
4) у =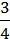 
х + 1;
5) у = 4;
6) у = х – 1,5.
786. Мотоцикліст рухається зі швидкістю 65 км/год. Задайте формулою залежність відстані s (у кілометрах), яку він подолає, від часу t (у годинах). Чи є ця залежність прямою пропорційністю?
787. Задайте формулою залежність:
1) довжини кола С від його радіуса r;
2) площі круга S, обмеженого цим колом, від радіуса r.
Яка із цих залежностей є прямою пропорційністю?
788. Запишіть формули двох будь-яких лінійних функцій, графіки яких проходять через точку Р(1; -5).
789. Графік якої з функцій проходить через точку (1; -4):
1) у = 4х;
2) у = 2х – 2;
3) у = 1;
4) у =-4;
5) у = -4х;
6) у =
Х – ?
790. Не виконуючи побудови графіка функції у = 1,8х – 7, з’ясуйте, чи проходить цей графік через точку:
1) А(0; 7);
2) В( 5; -16);
3) С(5; -2);
4) D(10; 11).
791. Не будуючи графіка функції у = -3х + 7, з’ясуйте, чи належить йому точка:
1) А(1; -4);
2) В(0; 7);
3) С(-1; 10);
4) D(10; -37).
792. Не виконуючи побудови, знайдіть нулі функції:
1) у = 2х – 6;
2) у = –
+ 8;
3) у = 7х;
4) у = -5х.
793. Не будуючи графіка, знайдіть нулі функції:
1) у = 4х + 12;
2) у = -8х.
794. Побудуйте графік прямої пропорційності:
1) у = х;
2) у = -2,5х;
3) у = – х;
4) у = Х.
795. Побудуйте графік прямої пропорційності:
1) у = 1,5х;
2) у = -2х.
796. Накресліть графік функції у = 5 – 2,5х. За графіком знайдіть:
1) значення функції, якщо значення аргументу дорівнює -4; 0; 2;
2) значення аргументу, якщо значення функції дорівнює -5; 0; 10;
3) нулі функції;
4) значення аргументу, при яких функція набуває додатних значень;
5) значення аргументу, при яких функція набуває від’ємних значень;
6) точки перетину графіка з осями координат.
797. Побудуйте графік функції у = 1,5х – 3. За графіком знайдіть:
1) яке значення у відповідає х = -2; 0; 4;
2) якому значенню х відповідає у = -3; 0; 6;
3) нулі функції;
4) значення аргументу, при яких функція набуває додатних значень;
5) значення аргументу, при яких функція набуває від’ємних значень;
6) точки перетину графіка з осями координат.
798. Знайдіть значення k, якщо графік функції у = kx – 2 проходить через точку (6; -11).
799. Знайдіть значення l, якщо графік функції у = – 
X + l проходить через точку M(10; -5).
800. Не виконуючи побудови, знайдіть координати точок перетину графіка функції з осями координат:
1) у = 1,5x – 20;
2) у = 5 – .
801. У яких точках перетинає осі координат графік функції:
1) у = 0,2x – 40;
2) у = 18 –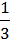 
X?
802. Точка А(0,7; 70) належить графіку прямої пропорційності. Задайте формулою цю функцію.
803. Задайте формулою пряму пропорційність, якщо її графік проходить через точку В( -2; 18).
804. Побудуйте графік функції:
1) y = (6 – х);
2) у = 
.
805. Побудуйте графіки функцій в одній системі координат та знайдіть координати точки їх перетину:
1) у – -0,5х – 1 і у = х – 4;
2) у = -2 і у = 3x – 5.
806. Побудуйте в одній системі координат графіки функцій у = 1,5x – 4 і у = 2 та знайдіть координати точки їх перетину.
807. Усі точки графіка функції y = kx + l мають одну й ту саму ординату, яка дорівнює 5. Знайдіть k і l,
808. Графік функції у = kx + l паралельний осі абсцис і проходить через точку М(0; -5). Знайдіть k і l.
809. Встановіть відповідність між формулами функцій у = 3x; у = -3x і у = x + 3 та їх графіками І-ІІІ, зображеними на малюнку 24.
810. Функцію у = 2х + 1 задано для -3 ≤ х ≤ 4. Знайдіть область значень цієї функції.
Мал. 24
811. Не будуючи графіка функції у = 4х – 6, знайдіть таку його точку, у якої:
1) абсциса дорівнює ординаті;
2) абсциса й ордината – протилежні числа;
3) абсциса вдвічі менша за ординату.
812. Побудуйте графік функції:
1) 
2) 
813. Побудуйте графік функції:
Вправи для повторення
814. Розв’яжіть рівняння:
1) (2х + 5)2 – (2х – 3)2 = 16;
2) (7х + 1)2 – (49х – 2)(х – 1) = -66.
815. Спростіть вираз:
1) (5m – 2)(5m + 2) – m(10m – 1) + (m – )2 ;
2) (а + 4y)2- (а – 2у)(а + 2у) – у(4а – 5у).
816. На столі лежать 73 зошити, а в коробці – 17 зошитів. Скільки зошитів треба перекласти зі стола в коробку, щоб у коробці їх стало вдвічі менше, ніж на столі?
817. Подайте вираз у вигляді квадрата двочлена, якщо це можливо:
1) 
Р2+ pq + 9p2;
2)
X2 – 
5xy = 
Y2;
3) 4х2 – 20ху – 25у2;
4) 36ab + 9а2 + 36b2.
Цікаві задачі для учнів неледачих
818. Стародавня аравійська задача. В Аравії помер старий чоловік. Усе своє майно, 17 верблюдів, він заповів своїм сином, причому старший мав одержати половину, середній – третину, а найменший – дев’яту частину цього майна. Після смерті батька сини не знали, що робити, бо 17 не ділилося без остачі ані на 2, ані на 3, ані на 9. Довго сперечалися брати, аж тут на верблюді під’їхав до них мудрець. Довідався про суперечку і дав братам мудру пораду, яка й допомогла розділити майно відповідно до батькового заповіту. Що саме порадив мудрець?
Домашня самостійна робота № 4
Кожне завдання мас по чотири варіанти відповідей (А-Г), серед яких лише один є правильним. Оберіть варіант правильної відповіді.
1. Яка з формул задає функцію?
A) х2 + у2 = ху;
Б) y = 
;
B) х2 + х + у – zy;
Г) у =
.
2. Яка з функцій є лінійною?
A) у = х – 2;
Б) у = 
;
B) у = х2 – 2;
Г) у = х3 – 2.
3. Яка з функцій задає пряму пропорційність?
A) у = х – 3;
Б) у = 
;
B) у = 2х;
Г) у = 2 + х.
4. Обчисліть значення функції у = 
для значення apгументу, що дорівнює -4.
А) 4;
Б) -4;
В) -5;
Г) 5.
5. Не виконуючи побудови, знайдіть нуль функції у = 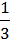х – 2.
А) 2;
Б) 4;
В) 6;
Г) -6.
6. На якому з малюнків зображено графік функції у = 3 – х?
А)
Б)
В)
Г)
7. Знайдіть область визначення функції у = 
.
A) Усі числа;
Б) усі числа, крім 0;
B) усі числа, крім 0 i 1;
Г) усі числа, крім 0 і -1.
8. Яка з точок належить графіку функції у = х2 – 2x?
А) (0; -2);
Б) (1; -1);
В) (-2; 0);
Г) (-1; -1).
9. Укажіть точку, у якій графік функції у = 0,1х + 15 перетинає вісь абсцис.
A) (0; 15);
Б) (150; 0);
B) (-150; 0);
Г) такої точки не існує.
10. Знайдіть для х – 2 значення функції
А) 4;
Б) 7;
В) 10;
Г) неможливо знайти.
11. Графік прямої пропорційності проходить через точку Р(2; -4). Укажіть точку, через яку також проходить цей графік.
А) (0; -2);
Б) (3; 6);
В) (-3; -6);
Г) (3; -6).
12. Не будуючи графіка функції у = 3х – знайдіть таку його точку, у якій абсциса й ордината є протилежними числами.
А) (-2; 2);
Б) (2; -2);
В) (4; -4);
Г) (-4; 4).
ЗАВДАННЯ ДЛЯ ПЕРЕВІРКИ ЗНАНЬ ДО & 19 – & 21
1. Які з даних формул задають функцію:
1) у = х2 + х;
2) у = 
;
3) у = 
;
4) ху = (х – y)2?
2. Чи є лінійною функція, яку задано формулою:
1) у = 3х – 7;
2) у = х2 – 5;
3) у = 4;
4) у = 
?
3. Лінійну функцію задано формулою:
1) у = -2х + 6;
2) у = 7,4х.
Для кожної із цих функцій назвіть коефіцієнти k і l.
4. Функцію задано формулою у – -2х і 7. Знайдіть:
1) значення функції, якщо значення аргументу дорівнює 5;
2) значення аргументу, якщо значення функції дорівнює 3.
5. Побудуйте графік функції у = 2х – 5. За графіком знайдіть:
1) значення функції для х = 4;
2) значення аргументу, при якому у = -3.
6. Функцію задано формулою у = 0,8х – 7,2. Не виконуючи побудови:
1) знайдіть нулі функції;
2) з’ясуйте, чи проходить графік функції через точку (10; 1).
7. Знайдіть область визначення функції у = 
.
8. Побудуйте в одній системі координат графіки функцій у = -2,5х і у = -5 та знайдіть координати їх точки перетину.
9. Знайдіть найменше значення функції у = х2 – 6х + 11.
Додаткові вправи
10. Функцію у = Зх – 7 задано для -2 ≤ х ≤ 5. Знайдіть область значень цієї функції.
11. Побудуйте графік функцій 
За графіком знайдіть:
1) нулі функції;
2) значення аргументу, при яких функція набуває додатних значень;
3) значення аргументу, при яких функція набуває від’ємних значень.
Вправи для повторення розділу 2
До& 19
819. Чи залежить площа квадрата від довжини його сторони? Чи є площа квадрата функцією від довжини сторони квадрата? Як можна задати що функцію, якщо сторона квадрата дорівнює а?
820. Функції задано формулами y= 
і g = 
. Заповніть таблицю, обчисливши відповідні значення функції:
X | -4 | -2 | 0 | 2 | 4 |
Y | |||||
G |
821. Із села до міста, відстань між якими дорівнює 48 км, вирушив велосипедист зі швидкістю 14 км/год. Задайте формулою залежність змінної 5 від змінної t, де s – відстань, яку велосипедисту залишилося проїхати до міста (у км), a t – час його руху (у год). За формулою знайдіть:
1) s, якщо t = 1,5;
2) t, якщо s = 13.
822. Знайдіть область визначення функції:
До & 20
823. Функцію задало формулою у – 2х – 3, де -2 ≤ х ≤ 3. Заповніть таблицю і побудуйте графік функції.
Х | -2 | -1,5 | -1 | 0,5 | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 |
У |
824. На малюнку 25 зображено графік функції.
За графіком знайдіть:
1) значення у, якщо х = -3; х = -1,5; х – 0; х = 1,5; х = 3;
2) значення х, яким відповідає у = -1,5; у = 2; у = 3;
3) область визначення функції;
4) область значень функції;
5) нулі функції;
6) значення аргументу, при яких функція набуває додатних значень;
7) значення аргументу, при яких функція набуває від’ємних значень.
Мал.25
825. Побудуйте графік функції:
1) у = |х|, де -2 ≤ х ≤ 4;
2) у = |х + 3|, де -5 ≤ х ≤ 3.
До &21
826. Які з даних функцій є лінійними? Які з них є прямою пропорційністю:
1) у = -3х;
2) у = -3х + 4;
3) у = -3х + 4х2;
4) у = -3;
5)у = – 
;
6)у = –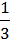Х?
827. Побудуйте графік функції:
1) у = 2х;
2) у = 1 – х;
3) у = 2;
4) у = 4х – 1;
5) у = -3х;
6) у = Х + 2.
828. Побудуйте графік прямої пропорційності у = – 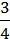Х. Знайдіть за графіком:
1) значения функції, якщо значення аргументу дорівнює 4; 0; 8;
2) значення аргументу, для якого значення функції дорівнює -6; 3; 6;
3) нулі функції;
4) значення аргументу, при яких функція набуває додатних значень;
5) значення аргументу, при яких функція набуває від’ємних значень.
829. Графіки функцій у = kx і у – 2х + l перетинаються в точці А(-2; 6). Знайдіть k і l.
830. На малюнках 26 і 27 зображено два графіки. Один з них описує процес наповнення резервуара водою, а другий – процес спорожнення резервуара від води. Який з малюнків відповідає кожному із вказаних процесів? По кожному з графіків знайдіть:
1) скільки літрів води було в резервуарі в початковий момент часу;
2) скільки літрів води буде в резервуарі через 1 хв; через 6 хв; через 8 хв від початку процесу;
3) через скільки хвилин від початку процесу в резервуарі буде 25 л води;
4) скільки літрів води надходить (виливається) щохвилини?
Задайте формулою залежність об’єму води V у резервуарі від часу t для кожного із цих двох процесів.
Мал. 26
Мал. 27
(2 votes, average: 4,00 out of 5)