Розділ 3 Відношення і пропорції
§21. Пропорція. Основна властивість пропорції
Відношення 12 : 3 і 20 : 5 рівні, оскільки їх значення дорівнюють 4. Тому можна записати рівність 
Рівність двох відношень називають пропорцією.
Слово “пропорція” походить від латинського proportio, що означає “співрозмірність”, тобто певне відношення частин між собою. За допомогою букв пропорцію записують так:
Ці пропорції можна прочитати так: “а, поділене на b, дорівнює с, поділеному на d”,
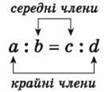
У пропорції а : b = с : d, або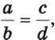 
а і d називають крайніми членами пропорції, а b і с – середніми членами пропорції:
Надалі будемо вважати, що всі члени пропорції відмінні від нуля: а ≠ 0, b ≠ 0, с ≠ 0, d ≠ 0.
Розглянемо пропорцію 
Використаємо основну властивість дробу: помножимо чисельник і знаменник дробу 
на d, а чисельник і знаменник дробу 
на b. Маємо: 
Отримані дроби є рівними, вони мають рівні знаменники, тому рівними будуть і їх чисельники: а ∙ d = с ∙ b.
Зауважимо, що а ∙ d – це добуток крайніх членів, а с ∙ b – добуток середніх членів пропорції. Прийшли до основної властивості пропорції.
– у пропорції 
добуток крайніх її членів дорівнює добутку середніх: ad = bc.
Приклад 1. Перевірити, чи є рівність 
пропорцією.
Розв’язання. І спосіб (за означенням пропорції). Оскільки 1,8 : 2 = 0,9 і 4,5 : 5 = 0,9, то рівність є пропорцією.
II спосіб (за основною властивістю пропорції). Оскільки 1,8 ∙ 5 = 9 і 2 ∙ 4,5 = 9, то рівність є пропорцією.
Приклад 2. Перевірити, чи можна з відношень 
скласти пропорцію.
Розв’язання. Оскільки 7 ∙ 4 = 28, 2 ∙ 13 = 26, а 28 Ф 26, то скласти пропорцію з даних відношень не можна.
Використовуючи основну властивість пропорції, можна знайти її невідомий член, якщо всі інші члени відомі.
Приклад 3. Знайти а з пропорції 4 : а = 5 : 12. Розв’язання. Використовуючи основну властивість пропорції, маємо: а ∙ 5 = 4 ∙ 12, 5а = 48, а = 48 : 5, а = 9,6.
Приклад 4. Розв’язати рівняння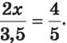 
Розв’язання. Використовуючи основну властивість пропорції, маємо: 2х ∙ 5 = 4 ∙ 3,5; 10х = 14; x = 14 : 10; х = 1,4.
Розглянемо пропорцію 
звідки 4 ∙ 12 = 8 ∙ 6.
Останню рівність можна одержати, очевидно, і з таких пропорцій:
(поміняли місцями середні члени заданої пропорції);
(поміняли місцями крайні члени заданої пропорції);
(поміняли місцями середні та крайні члени за даної пропорції).
Звідси випливає, що середні члени або (та) крайні члени пропорції можна міняти місцями.
А ще раніше…
У IV ст. до н. е. загальну теорію пропорційності розглянули давньогрецькі вчені, зокрема Тестет та Евдокс. Цю теорію було детально викладено у п’ятій книзі “Начал” Евкліда.
У сьомій книзі “Начал” Евклід виклав теорію відношень та пропорцій для цілих чисел. Так, зокрема, у її 19-му реченні Евклід доводить основну властивість пропорції.
Також з пропорції a : b = c : d Евклід виводить такі:
B : a = d : c; (a + b) : b = (c + d) : d;
A : c = b : d; (a – b) : b = (c – d) : d;
A : (a – b) = c : (c – d).
Що таке пропорція? э У пропорції m : n = p : k назви крайні члени, середні члени. Сформулюй основну властивість пропорції. Які перестановки членів пропорції можна виконувати?
527. (Усно) Чому рівність 
є пропорцією? Назви її крайні члени і середні члени.
528. (Усно) Чому з відношень 
не можна скласти пропорцію?
529. У пропорції 25 : 5 = 60 : 12 вкажи крайні члени, середні члени.
530. Запиши у вигляді пропорції твердження:
1) 7, поділене на 2, дорівнює 14, поділеному на 4;
2) 2 відноситься до 3, як 10 відноситься до 15;
3) відношення а до 2 дорівнює відношенню 3 до 7.
531. Запиши у вигляді пропорції твердження:
1) 2, поділене на 5, дорівнює 8, поділеному на 20;
2) відношення 4 до 2 дорівнює відношенню 6 до 3;
3) х відноситься до 5, як у відноситься до 7.
532. Перевір, користуючись означенням, чи можна з даних відношень скласти пропорцію:
1) 11,2 : 3,2 і 15,75 : 4,5;
533. Перевір, користуючись означенням, чи можна з даних відношень скласти пропорцію:
1) 0,7 : 0,1 і 0,8 : 0,2;
534. Перевір, користуючись основною властивістю пропорції, чи можна з даних відношень скласти пропорцію:
535. Перевір, користуючись основною властивістю пропорції, чи можна з даних відношень скласти пропорцію:
536. Знайди рівні між собою відношення і склади з них пропорції:
27 : 9; 5 : 15; 28 : 4; 4 : 12; 
3 : 1.
537. Знайди рівні між собою відношення і склади з них пропорції: 
538. Знайди невідомий член пропорції:
1) х : 6 = 2 : 3; 
539. Знайди невідомий член пропорції:
1) х : 4 = 5 : 25; 
540. З пропорції:
утвори нову, помінявши місцями крайні члени;
утвори нову, помінявши місцями середні члени.
541. З пропорції 
утвори нові, переставивши місця ми крайні або середні члени.
542. Розв’яжи рівняння:
543. Розв’яжи рівняння:
544. Використовуючи рівність 4 ∙ 5 = 2 ∙ 10, запиши усі можливі пропорції.
545. З чисел 8, 4, 3 і 6 склади пропорцію.
546. Знайди відношення х до у, якщо: 
547. Склади дві пропорції, добуток крайніх членів яких дорівнює 16.
548. При якому значенні у є правильною пропорція:
549. Розв’яжи рівняння:
550. Відомо, що 
Доведи, що: 
Розв’язання. 1) 
Віднімемо одиницю від обох частин рівності: 
Рівність доведено.
551. До чисел 10, 5 і 4 добери четверте так, щоб можна було скласти пропорцію (розглянь усі випадки).
552. Велосипедист, що рухається зі швидкістю 12 км/год, подолав відстань між двома селами за 0,75 год. За який час подолає цю відстань пішохід, що рухається зі швидкістю 5 км/год?
553. Заповни таку таблицю в зошиті за зразком:
554. 96 команд грають у баскетбольному турнірі за олімпійською системою, тобто нічиїх немає, команда, що програє матч, – зі змагань вибуває. Скільки буде проведено матчів, щоб виявити переможця?
(1 votes, average: 5,00 out of 5)