УРОК № 57
Тема. Сума перших n членів геометричної прогресії
Мета уроку: закріпити знання учнів про зміст означення та супутніх понять геометричної прогресії, а також про її основні властивості. Доповнити ці знання знанням формули n-го члена геометричної прогресії.
Закріпити вміння: вирізняти геометричну прогресію серед числових послідовностей, відшукувати знаменник геометричної прогресії, перші члени геометричної прогресії, а також використовувати властивості геометричної прогресії. Сформувати вміння записувати формулу
Тип уроку: доповнення і закріплення знань, відпрацювання вмінь та навичок.
Наочність та обладнання: опорний конспект № 35.
Хід уроку
І. Організаційний етап
Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.
II. Перевірка домашнього завдання
Оскільки вправи домашнього завдання за змістом, способом розв’язування, а також рівнем складності відповідають вправам, розв’язаним на попередньому уроці, то ретельній перевірці підлягають тільки письмові
Фронтально учні можуть виконати тестові завдання [9, тест 21], продемонструвавши рівень володіння основними питаннями теми “Геометрична прогресія”.
ІІІ. Формулювання мети і завдань уроку.
Мотивація навчальної діяльності учнів
Можливі помилки при виконанні тестових завдань на попередньому етапі уроку мають переконати учнів у необхідності подальшого опрацювання матеріалу попереднього та інших уроків в напрямі закріплення знань та вироблення сталих умінь використовувати ці знання як в стандартних, так і в нестандартних ситуаціях. Це твердження виражає основну мету уроку.
IV. Актуалізація опорних знань та вмінь учнів
Усні вправи
1. Яка послідовність називається геометричною прогресією? Наведіть приклад.
2. Чому дорівнює відношення двох сусідніх членів геометричної прогресії, починаючи з другого?
3. Як задати геометричну прогресію?
4. Як записується формула п-го члена геометричної прогресії?
5. Як записується формула суми перших л членів геометричної прогресії, якщо відомі:
1) її перший член і знаменник;
2) її перший член, знаменник і n-й член?
V. Відпрацювання вмінь
Письмові вправи
Зміст письмових вправ уроку може бути таким:
1) задачі на відшукання суми послідовних членів геометричної прогресії з n-го по m-й включно (n < m) та задачі, що зводяться до цього;
2) задачі на застосування вивчених формул для відшукання невідомих першого члена, або знаменника, або кількості n членів геометричної прогресії за відомою за умовою сумою її перших членів;
3) прикладні задачі на застосування вивчених на попередніх чотирьох уроках формул для геометричної прогресії;
4) на повторення: задачі на застосування формул для арифметичної прогресії.
VI. Підсумки уроку
Учні узагальнюють основні типи задач на застосування формул для обчислення суми перших n членів геометричної прогресії.
VII. Домашнє завдання
1. Повторити зміст матеріалу за опорними конспектами № 33-35.
2. Виконати самостійну роботу (див. нижче) за варіантом, указаним учителем.
Самостійна робота
Варіант 1
Знайдіть суму:
1) перших п’яти членів геометричної прогресії (bn), якщо b1 = 8, q = 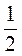 ;
;
2) перших шести членів геометричної прогресії (bn):  ;
;  ;
;  ; … ;
; … ;
3) перших семи членів геометричної прогресії (bn), якщо вона задана формулою загального члена bn = 3 • 2n+1;
4) перших п’яти членів геометричної прогресії (bn), якщо сума другого і третього її членів дорівнює -12, а різниця четвертого і другого членів дорівнює 48.
Варіант 2
Знайдіть суму:
1) перших п’яти членів геометричної прогресії (bn), якщо b1 = 625, q = 0,2;
2) перших шести членів геометричної прогресії (bn): 18; 24; 32; …;
3) перших п’яти членів геометричної прогресії (bn), якщо вона задана формулою загального члена bn = 5 • 2n-1;
4) перших п’яти членів геометричної прогресії (bn), якщо різниця третього і другого її членів дорівнює 6, а різниця четвертого і другого членів дорівнює 30.

 (2 votes, average: 4,50 out of 5)
(2 votes, average: 4,50 out of 5)