Урок № 44
Тема. Функція 
, її властивості і графік
Мета: домогтися засвоєння учнями змісту основних властивостей функції ; сформувати вміння відтворювати вивчені властивості, а також використовувати їх у розв’язуванні програмових задач.
Тип уроку: засвоєння знань та вмінь.
Наочність та обладнання: опорний конспект “Функції”.
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
На цьому етапі проводимо самостійну роботу за матеріалом
Самостійна робота 9
Варіант 1 | Варіант 2 |
1. Спростіть вирази: | |
А) Б) | А) Б) |
2. Виконайте дії: | |
А) Б) В) | А) Б) В) |
3. Скоротіть дріб: | |
А) | А) |
;
.
;
.
;
;
.
;
;
class=""/>.
; б) 
.
; б) 
.III. Формулювання мети і завдань уроку
Логіка вивчення матеріалу курсу алгебри 8 класу, а звідси й мета уроку, встановлюється дуже легко, якщо запропонувати учням розв’язати логічну вправу.
Логічна вправа:
Який запис пропущено?
Раціональний дріб |
|
Квадрат числа | У = х2 |
Квадратний корінь | ? |
Після проведення аналізу даних завдання та встановлення логічних зв’язків між поняттями (певний вид виразу – відповідна функція) учні мають усвідомити, що по закінченні вивчення властивостей арифметичного квадратного кореня та їх застосування важливим с питання про вивчення властивостей функції . Таким чином формулюється дидактична мета уроку: повторивши вивчені властивості арифметичного квадратного кореня, сформулювали загальні властивості відповідної функції , засвоїти форму її графіка та сформувати первинні вміння застосовувати вивчені властивості в розв’язуванні задач.
IV. Актуалізація опорних знань та вмінь
@ З метою успішного сприйняття навчального матеріалу слід активізувати такі знання і вміння учнів: означення і властивості арифметичного квадратного кореня з числа; знаходження ОДЗ виразу 
; читання графіків функцій (за готовим зображенням графіка знайти значення функції, якщо задане значення аргументу, або навпаки, знайти, при якому значенні аргументу функція набуває даного значення); графічне розв’язування рівнянь виду f(х) = g(x); виконання найпростіших побудов у декартовій системі координат.
Виконання усних вправ
1. При яких значеннях змінної а не мають змісту вирази: 
; 
; 
; 
; 
; 
; 
; 
; 
?
2. Визначте знак виразів (найменше або найбільше значення): ; 
; 
; 
.
3. Дано функцію у = 5х2 – 1. Чи належать графіку цієї функції точки А(1; 4); В(-1; -6); С(0; -1)?
4. Який із рисунків відповідає графічному способу розв’язання рівняння 
?
А) | Б) | В) | Г) |
|
|
|
|
V. Засвоєння знань
План вивчення нового матеріалу
1. Уявлення про задачі, що приводять до функції .
2. Побудова графіка функції ; його порівняння з правою віткою графіка функції у = х2.
3. Дослідження властивостей функції .
4. Приклади застосування властивостей функції .
@ На передостанньому уроці вивчення теми “Квадратні корені” учні повторюють набуті на попередніх уроках знання про означення і властивості арифметичного квадратного кореня з числа, на основі чого формують уявлення про властивості і графік функції , порівнюють його з графіком функції у = х2 при х? 0 і встановлюють їх симетричність відносно прямої у = х. (Цей факт можна встановити різними способами: або проаналізувавши (повторивши) попередньо властивість взаємного розташування точок з координатами (а; b) і (b; а), або попрацювавши з рисунком, учні, маючи зображення графіків функції та у = x2 на окремому рисунку, можуть переконатися в симетричності графіків, просто перегнувши рисунок по прямій у = х).
Вивчаючи питання про властивості функції , традиційно звергаємо увагу на область визначення (х? 0), область значень (у? 0), положення графіка в системі координат (І чверть), а також властивість, яку до цього уроку використовували на інтуїтивному рівні: більшому значенню аргументу (підкореневому виразу) відповідає більше значення функції (значення арифметичного квадратного кореня) (докладніше про монотонність функції та її види учні будуть говорити пізніше – у 9-му класі, але на цьому уроці вчитель може повідомити учням її назву – зростання функції).
VI. Формування вмінь
Виконання усних вправ
1. Порівняйте: 
і 
; 8 і 
; 
і 0; 10 і 
; 
і – 3; 
і 5.
2. Функцію задано формулою . Заповніть порожні клітинки таблиці:
X | 1 | 5 |
| |
Y | 5 | 0 |
| 2 |
3. Який із рисунків відповідає графічному способу розв’язання рівняння 
?
А) | Б) | В) | Г) |
|
|
|
|
Виконання письмових вправ
Для реалізації дидактичної меш на цьому уроці слід виконати завдання такого змісту:
1. Читання графіка функції .
1) Користуючись графіком функції , знайдіть значення функції, які відповідають таким значенням аргументу: 3; 2,5; 0,75; 5.
2) Користуючись графіком функції , знайдіть:
А) значення при х = 2,5; 5,5; 8,4;
Б) значення х, якому відповідає 
; 1,7; 2.5.
2. Застосування монотонності функції .
1) За допомогою графіка функції порівняйте числа: а) 
і 
; б) 
і 
; в) 
і 
.
2) Що більше: а)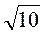 
чи 
; б) 
чи 
; в) 
чи 
; г) 7 чи ; д) чи 8; є) 
чи 1,4?
3. Перевірка обчисленням, чи належить точка із заданими координатами графіку функції .
1) Чи належать графіку функції точки: A(50; 5); B(36; 6); D(3; 9)?
2) Чи належать графіку функції точки: A(64; 8); B(10000; 100); С(-81; 9); D(25; -5)?
4. Побудова фрагменту графіка функції (для вказаних значень аргументу). Побудуйте графік функції , де 1 ? х? 9.
5. Графічне розв’язування рівняння виду 
та 
.
Розв’яжіть графічно рівняння: а) 
; б) 
.
6. Логічні вправи та завдання підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.
1) Побудуйте графік функції, яку задано формулою: а) 
; б) 
; в) 
; г) 
.
2) Знайдіть пропущений вираз.
7. На повторення: завдання, що передбачають виконання тотожних перетворень виразів, що містять арифметичний квадратний корінь.
1) Спростіть вираз: а) 
; б) 
; в) 
; г) 
.
2) Доведіть, що значення виразу є числом раціональним: а) 
; б) 
.
3) Знайдіть значення виразу: а) 
; б) 
; в) 
; г) 
.
@ Система завдань, присвячених засвоєнню властивостей функції у = 4х, така сама, як і система вправ на засвоєння властивостей інших функцій. Враховуючи місце уроку в темі, бажано на уроці виконати завдання на повторення найбільш складних моментів тотожних перетворень виразів, що містять арифметичний квадратний корінь.
VII. Підсумки уроку
В якому з випадків правильно зображено графік функції?
Б) 
В) 
VIII. Домашнє завдання
1. Вивчити властивості функції , вид та властивості її графіка.
2. Розв’язати вправи на закріплення вивчених властивостей функції .
3. На повторення: розв’язати завдання на використання властивостей арифметичного квадратного кореня, видів перетворень виразів, що містять квадратні корені.
(1 votes, average: 5,00 out of 5)