1.
1) Вектор паралельного перенесення, що переводить відрізок ОА в СВ:
 Вектор, що переводить відрізок ОС в АВ:
Вектор, що переводить відрізок ОС в АВ: 
2) Вектор, що переводить ОС в АВ:  Вектор, що переводить О А в СВ:
Вектор, що переводить О А в СВ: 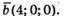
3) Вектор, що переводить ОС в АВ:  Вектор, що переводить ОА в СВ:
Вектор, що переводить ОА в СВ: 
4) Вектор, що переводить ОС в АВ:  Вектор, що переводить ОА в СВ:
Вектор, що переводить ОА в СВ: 
2.
Знайдемо координати
1) х1 = 0 + 1 = 1; у1 = -1 + (-2) = -3; 
2) х1 = 2 + 1 = 3; у1= -3 + (-2) = -5; 
3) 0 = х + 1; х = -1; -1 = у – 2; у = 1; 
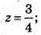
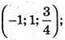
4) -8 = х + 1; х – -9; 4 = у – 2; у = 6; 

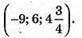
3.
Знайдемо координати точки С – середини відрізку АВ.


 С(3,5; 1; 3).
С(3,5; 1; 3).
Знайдемо координати вектора паралельного перенесення, враховуючи те,
Що точки С
0 = 3,4 + ах; ах = -3,5; 0 = 1 + а; а = -1; 0 = 3 + аz; аz = -3; 
Знайдемо координати точок, у які перемістилися кінці відрізка АВ.
X1 = 2 – 3,5 = -1,5; у1 = -3 – 1 = -4, z1 = 5 – 3 = 2; А1(-1,5; -4; 2);
X1 = 5 – 3,5 – 1,5; у. – 5 – 1 = 4; z1= 1 – 3 = -2; В1(1,5; 4; -2).
6.
Нехай точка А(x; у; z) належить сфері. З’ясуємо, в яку точку
Перейде А при паралельному перенесенні на 
Х 1 = х – 11; х = х + 11; у 1 = у + 5; у = у1 – 5; z 1 = z + 13; z = z 1 – 13.
Підставимо координати в рівняння сфери.
(x 1 + 11)2 + (у 1, – 5 – 1)2 + (z 1- 13 + 1)2 = 4;
(x1 + 11) + (у1 – 6)2 + (z 1 – 12)2 = 4 – рівняння сфери,
Отриманої паралельним перенесенням.
7.
Нехай точка А(x; у; z) належить отриманій сфері.
З’ясуємо координати прообразу цієї точки х = x 1- 1; у = у 1 + 1; z = z 1 + 3.
Підставимо координати в рівняння сфери.
(x 1 – 1)2 + (у 1 + 1 +1)2 + (z + З)2 = 4;
(x 1 – 1)2 + (у 1 + 2)2 + (z + 2)2 = 4 – рівняння сфери-прообразу.
8.
Нехай точка А(х; у; z) належить площині.
З’ясуємо, в яку точку перейде А при паралельному перенесенні на 
X1 = х – 1; x = х1 + 1; у 1 = у + 5; у = у 1 – 5; z 1 = z + 3; z = z 1 – 3.
Підставимо координати в рівняння площини.
3(x 1 + 1) – (у 1 – 5) + 8(z 1 – 3) – 17 = 0; Зx1 + 3 – у 1 + 5 + 8z 1 – 24 – 17 = 0;
Зx 1 – у 1 + 8z 1 – 33 = 0 – рівняння образу площини.
9.
Нехай точки А(а; у; z) належить отриманої площині. x = x1 + 1; у = у1 – 1; z = z1 + 2.
Підставимо координати в рівняння площини x 1 + 1 – 2(у 1 – 1) + 3(z 1 + 2) + 1 = 0;
Х1 + 1 – 2у1 + 2 + Зz1 + 6 + 1 = 0;
X1 – 2у1 + Зz1 + 10 = 0 – рівняння площини – прообразу.
10.
Знайдемо координати точки С – центра симетрії відрізка.


 С(0; 3; 0,5).
С(0; 3; 0,5).
11.
1) Знайдемо координати точки М1, що симетрична точці М( 1; 2; -3)
Відносно початку координат.
 х = -1;
х = -1;  y = – 2;
y = – 2;  z = 3; М 1 (-1; -2; 3).
z = 3; М 1 (-1; -2; 3).
2) Знайдемо координати точки М1, що симетрична точці М(1; 2; -3)
Відносно точки
 х = -3;
х = -3;  y = 2;
y = 2;  z = 5; М1(-3; -2; 5).
z = 5; М1(-3; -2; 5).
3) Знайдемо координати точки М1, що симетрична точці М( 1; 2; -3)
Відносно точки
Р(5; -5; 4),  х = 9;
х = 9; 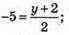 y = -2;
y = -2;  z = 11; М 1 (9; -12; 11).
z = 11; М 1 (9; -12; 11).
14.
Геометричним місцем точок центрів симетрії двох даних паралельних
Площин буде площина паралельна даним і рівновіддалена від них.
16.
1) Нехай точка А(x; у; z) належить площині x + у + z – 3 = 0.
Знайдемо точку А1 симетричну точці А відносно точки Р(2; 2; 2).
 х = 4 – х1;
х = 4 – х1;  y = 4 – у1;
y = 4 – у1; 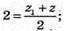 z = 4 – z1.
z = 4 – z1.
Підставимо координати в рівняння площини.
(4 – x1) + (4 – у1) + (4 – z1) – 3 = 0; – x1 – у1 – z1 + 12 – 3 = 0; – x1 – у1 = z1 + 9 = 0;
X1 + у1 + z1 – 9 = 0 – рівняння симетричної площини.
2) Нехай точка А(х; у; z) належить площині х + у + z – 3 = 0.
Точка А1(x1; у1; z1) симетрична точці А відносно точки O(0; 0; 0), а значить:
 х = – x1
х = – x1 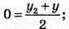 y = – у1
y = – у1  z = – z1.
z = – z1.
Підставимо координати в рівняння площин:
– x1 – у1 – z1 – 3 = 0; x1 + у1 + z1 + 3 = 0 – рівняння симетричної площини.
3) Нехай точка А(х; у; z) належить площині х + у + z – 3 = 0.
Точка А1(x1; у1; z1) симетрична точці А відносно точки H(1; -1; 2), а значить:
 x = 2 – x1,
x = 2 – x1,  y = -2 – у1;
y = -2 – у1;  z = 4 – z1.
z = 4 – z1.
Підставимо координати в рівняння площини.
(2 – x1) + (-2 – у1) + (4 – z1) – 3 – 0; 2 – x1 – 2 – у1 + 4 – z1 -3 = 0; x1 – у1 – z1 + 1 = 0;
X1+ у1 + z1 – 1 = 0 – рівняння симетричної площини.
17.
Площини х + y + z – 3 = 0 і х = y + 2 – 9 = 0 паралельні.
Геометричне місце точок центрів симетрії цих площин – це площина
Паралельна заданим площинам і рівновіддалена від них, тому задача
Має безліч розв’язків, це всі точки, що належать паралельній,
Рівновіддаленій площині.
18.
Знайдемо довжину відрізку АВ. 
Розглянемо два випадки.
В першому випадку координати двох інших вершин квадрату
С(4; 0; 5), D(8; 3; 5).
В другому – С(4; 0; -5), D(8; 3; -5).
Знайдемо координати вершин квадрату, який симетричний відносно точки
(2; 2; 2).
В першому випадку:
 х = 0;
х = 0;  у = 4;
у = 4;  z = 4. А1(0; 4; 4) – точка симетрична точці А.
z = 4. А1(0; 4; 4) – точка симетрична точці А.
 х = -4;
х = -4;  у = 1;
у = 1;  z = 4. В1(-4; 1; 4) – точка симетрична точці В.
z = 4. В1(-4; 1; 4) – точка симетрична точці В.
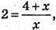 х = 0;
х = 0;  y = 4;
y = 4; 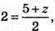 z = -1. C1(0; 4; -1) – точка симетрична точці С.
z = -1. C1(0; 4; -1) – точка симетрична точці С.
 х = -4;
х = -4;  y = 1;
y = 1;  z = -1. D1(-4; 1; -4) – точка симетрична точці В.
z = -1. D1(-4; 1; -4) – точка симетрична точці В.
В другому випадку:
 х = 0;
х = 0;  y = 4
y = 4  z = 4. А1 (0; 4; 4) – точка симетрична точці А.
z = 4. А1 (0; 4; 4) – точка симетрична точці А.

 х = -4;
х = -4;  y = 1;
y = 1;  z = 4. В1 (-4; 1; 4) – точка симетрична точці В.
z = 4. В1 (-4; 1; 4) – точка симетрична точці В.
 х = 0;
х = 0;  y = 4;
y = 4; 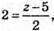 z = 9. С1(0; 4; 0) – точка симетрична точці С.
z = 9. С1(0; 4; 0) – точка симетрична точці С.
 х = -4;
х = -4;  y = 1;
y = 1; 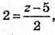 z = 9. D1(-4; 1; 9) – точка симетрична точці D.
z = 9. D1(-4; 1; 9) – точка симетрична точці D.
19.
1) Завжди існує площина, відносно якої є симетричними дві точки.
2) Не завжди існує площина, відносно якої є симетричними дві прямі.
Наприклад, розглянемо дві мимобіжні прямі.
3) Завжди існує площина, відносно якої є симетричними дві площини.
20.
Ні, дане твердження є невірним. Якщо площини (прообраз і площина симетрії)
Не паралельні, то не будуть паралельними і прообраз і образ.
21.
Проведемо переріз, який проходить через висоту піраміди і
Перпендикулярний основі. В перерізі отримаємо трикутник,
А він має центр симетрії.
22.
Оскільки прямі m і n симетричні відносно площини, то кут нахилу
Прямої n до площини дорівнює куту нахилу прямої m до площини.
Таким чином, кут між прямою n і площиною дорівнює 36º,
А кут між прямими піт дорівнює 36º · 2 = 72º.
23.
1) Кут має три площини симетрії, які проходять через середини
Протилежних ребер, та перпендикулярні їм, а також через площини симетрії,
Які проходять через протилежні ребра верхньої та нижньої основи.
2) Правильна трикутна піраміда має три площини симетрії (проходить
Через бічне ребро, перпендикулярно протилежному ребру основи).
25.
Якщо послідовно сполучити кінці цих відрізків, то отримаємо рівнобічну трапецію.
26.
1) Вектором-нормаллю даної площини буде  Тоді відповідний шуканій
Тоді відповідний шуканій
Точці М радіус-вектор колінеарний до n(1; – 2; 1), отже, М(а; -2а; а).
Знайдемо а з умови, що точки (0; 0; 0) і (а; -2а; а) рівновіддалені від площини
Х – 2у + z -3 = 0. d((0;0;0); 
D((a;-2a; а);  6a – 3 = 3
6a – 3 = 3  ¦6a-З¦ = 3.
¦6a-З¦ = 3.
Або 6а – 3 = -3; 6а = 6 або 6а = 0; а = 1 або а = 0.
Точка М має координати (1; -2; 1).
2) Паралельним перенесенням  Перетворимо точку М(1; 1; 1) на O(0; 0; 0).
Перетворимо точку М(1; 1; 1) на O(0; 0; 0).
При такому перетворенні маємо: х1 = х – 1, х = x1 + 1; у1 = у – 1, у = у1 = 1;
Z1 = z – 1, z = z1 +1.
Підставимо в рівняння площини: x1 +1- 2(у1 + 1) + z1 + 1 – 3 = 0;
X1- 2у1 + z1 – 3 = 0. Тобто площина при цьому перетворенні переходить сама в себе. Точка симетрична точці О відносно даної площини O1(1; -2; 1) (див. 1).
Оберненим перетворенням паралельного перенесення  Шукану точку (0; -3; 0).
Шукану точку (0; -3; 0).
3) Паралельним перенесенням  перетворимо точку М(-1; 0:1) на O(0; 0; 0).
перетворимо точку М(-1; 0:1) на O(0; 0; 0).
При такому перетворенні маємо: x1 = х + 1; x = х1 – 1; у1 = y; y = y1;
Z1 = z – 1, z = z1 + 1.
Підставимо в рівняння площини: x1 – 1 – 2 у1 + z1 + 1 – 3 = 0; x1 – 2у1 + z1 – 3 = 0.
Тобто площина при цьому перетворенні переходить сама в себе.
Точка симетрична точці О відносна даної площини О 1(1; -2; 1) (див. 1).
Оберненим перетворенням паралельного перенесення 
Отримаємо шукану точку (2; -2; 0).
28.
1) Трикутна призма має поворотну ось симетрії, якщо вона правильна.
2) Тетраедр має поворотну ось симетрії, якщо він правильний.
3) Правильний тетраедр має поворотну ось симетрії.
4) Довільна піраміда не має поворотних осей симетрії.
5) Правильна піраміда має поворотну ось симетрії.
29.
Утворена фігура є паралелепіпедом. Він має 6 граней.

32.
Точки симетричні відносно осі аплікат повинні мати протилежні за знаком
Абсцису та ординату, а аплікати мають бути рівними, тому координатні формули:
X1 = – х, у1 = у, z1 = z.
33.
Вісь Оz збігається з віссю повороту. Тоді центр даної сфери 
Перетвориться поворотом на 60° відносно Оz в точку А 1(x1; у1; z1),
Де 
 z1 = 0.
z1 = 0. 
Маємо: x1= 2 cos 0° = 2; y1 = 2 sin 0º = 0; z1 = 9.
Маємо рівняння сфери (x – 2)2 + у2 + z2= 4.
34.
AB3C3D3A2B2C2D2 – паралелепіпед гомотетичний даному з центром
Гомотетії в вершині А і коефіцієнтом гомотетії 
Лінійні розміри цих паралелепіпедів відноситься як 1:3,
Отже їх площі будуть відноситися як 1:9.

36.
1) Знайдемо рівняння сфери гомотетичної даній з коефіцієнтом 1,2
Відносно початку координат. В такому випадку координати точки образу
М(x1; у1; z1) прообразу
М(х; у; z) пов’язані співвідношенням: 
Координати центра даної сфери O(-1; 2; 3).
Тоді координати центра O1 шуканої сфери О1(1,2; 2,4; 3,6).
Радіус даної сфери дорівнює 3. Тоді радіус шуканої сфери дорівнює
1,2 х 3 = 3,6. Рівняння шуканої сфери: (х + 1,2)2 + (у – 2,4)2 + (z – 3,6)2= 3,62.
2) Знайдемо рівняння сфери гомотетичної даній з коефіцієнтом 1,2
Відносно точки (1; 1; 1). Паралельним перенесенням на вектор І
І
Відобразимо центр гомотетії у початок координат.
Тоді центр даної сфери О(-1; 2; 3) відобразиться у точку О1(-2; 1; 2).
Перетворенням гомотетії відносно початку координат з коефіцієнтом 1,2 точка
О1(-2; 1; 2) перетвориться на точку О2(-2,4; 1,2; 2,4).
Після оберненого паралельного перенесення на вектор  Отримаємо
Отримаємо
Координати центра шуканої сфери О3(-1,4; 2,2; 3,4).
Радіус шуканої сфери 3 х 1,2 = 3,6.
Запишемо рівняння сфери з центром (-1,4;· 2,2; 3,4) і радіусом 3,6.
(х + 1,4)2 + (у – 2,2)2 + (z – 3,4)* = 3,62.
3) Знайдемо рівняння сфери гомотетичної даній з коефіцієнтом 1,2
Відносно центра даної сфери.
В цьому випадку центр шуканої сфери матиме такий же центр (-1; 2; 3),
А радіус її 1,2 х 3 = 3,6.
Запишемо рівняння шуканої сфери: (x + 1)2+ (у – 2)2 + (z – З)2 = 3,62.
37.
1) Знайдемо рівняння площини, гомотетичної площині х – 2у + z – 3 = 0
З коефіцієнтом k = -0,5 відносно початку координат.
При перетворенні подібності рівняння площини образу відрізняється
Від рівняння площини прообразу тільки вільним членом –
Він змінюється в k разів. Шукане рівняння має вигляд;
Х – 2у + z – З • (-0,5) = х – 2у + z + 1,5 = 0.
2) Знайдемо рівняння площини, гомотетичної площині х – 2у + z – 3 = 0
З коефіцієнтом k = -0,5 відносно точки (0; -2: 1).
Паралельним перенесенням на вектор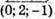 відобразимо центр гомотетії
відобразимо центр гомотетії
У початок координат.
Це перетворення задається співвідношенням:
 Звідси
Звідси 
Підставимо в рівняння площини: x1 + 2(у1 – 2) + z1 + 1 – 3 = 0; x – 2у1 + z1 +2 = 0.
При перетворені подібності рівняння площина образу і прообразу
Відрізняються вільним членом – він змінюється в k разів.
Отримуємо рівняння: х1 – 2y1 + z1 + 2 х (-0,5) = х – 2 y1 + z1 – 1 = 0.
Виконуємо перехід до координат z, y, z. X – 2(у + 2) + z – 1 – 1 = 0;
Х – 2у + z – 6 = 0 – рівняння шуканої площини.
3) Знайдемо рівняння площини, гомотетичної площині
X – 2y + z – 3 = 0 з коефіцієнтом k = -0,5 відносно точки (-4: 3: 2).
Паралельним перенесенням на вектор відобразимо центр
відобразимо центр
Гомотетії у початок координат.
Це перетворення задається співвідношеннями
 Звідси
Звідси 
Підставимо в рівняння площини: х1 – 4 – 2(у1 + 3) + z1 + 2 – 3 = 0;
Х1 -2 y1+ z1 – 11 = 0. При перетворенні подібності рівняння площин образу
І прообразу відрізняються вільним членом – він змінюється в k разів.
Отримуємо рівняння: х1 – 2 y1 + z1 – 11 • (-0,5) = 0; х1 – 2y1 + z1 + 5,5 = 0.
Виконуємо перехід до координат x, у, z. (x + 4) – 2(у – 3) + (z – 2) + 5,5 – 0; x – 2y + z + 13,5 = 0 – рівняння шуканої площини.
