Урок № 11
Тема. Повторення відомостей про звичайні дроби. Основна властивість дробу
Мета: повторити відомості про звичайні дроби, набуті в 5 класі (зміст чисельника і знаменника звичайного дробу, запис, читання; дріб як частка; порівняння [додавання і віднімання дробів з однаковими знаменниками], види дробів: правильний і неправильний; запис неправильного дробу і мішане число і т. ін.); сформувати в учнів уявлення про рівність дробів (з однаковими знаменниками).
Тип уроку: повторення й систематизація знань.
Хід уроку
І.
Учитель повідомляє про те, що одним з основних понять, які вивчає математика, є поняття числа; учні вже знайомі з цим поняттям і знають, що числа бувають натуральними (використовуються для лічби) і дробовими (означають частину числа або суму натурального і дробового чисел). У 5 класі вони вже познайомилися з різними видами дробів. Для актуалізації опорних знань учнів пропонуються види вправ (на вибір учителя).
Далі учитель може запропонувати:
Усні вправи
Прочитайте дроби: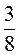 
, 
, 
. Назвіть їх
Порівняйте чисельник і знаменник кожного дробу. Про що свідчать ці нерівності?
Яке значення а задовольняє одночасно всі умови: 
; 
; 
?
Заповніть порожні квадратики числами, щоб рівність була правильною: 
.
Заповніть квадратики так, щоб рівності були правильними: 
; 
.
Ігровий момент “Аукціон”
Учитель “виставляє” на “аукціон” три “лоти”:
Лот № 1 Лот № 2 Лот № 3
Завдання: “перебити ціну” іншого учня, тобто всі бажаючі по черзі називають, що вони знають про кожне із записаних чисел. Перемагає той учень, який назве останню властивість дробу.
II. Систематизація та узагальнення знань
@ Після такої активної “розминки” (див. п. 1) учні зазвичай дуже легко сприймають традиційні в цій темі пояснення вчителя на менш складних або на більш простих прикладах. Поділимо круг на чотири рівні частини, три з яких зафарбуємо, а потім кожну чверть круга поділимо ще на п’ять рівних частин (рис. 1).
Тоді все коло буде поділено на 4 – 5 = 20 частин, а третина всіх зафарбованих частин круга буде 3 – 5 таких, частин. Тому 
, тобто 
або 
.
Альтернативний варіант викладення теми може бути таким.
Згадаємо, що дріб – це частка відділення чисельника на знаменник, а частка не зміниться за умови збільшення (або зменшення) діленого і дільника в одну й ту саму кількість разів.
У будь-якому разі учні доходять висновків, записаних у конспект 7.
Конспект 7 | |
Основна властивість дробу | |
1) 2) рівні дроби є різними записами одного й того самого числа | Приклад
|
або 
;
;
.@ Для зацікавлених учнів можна пояснити, що й ділення, і множення чисельника і знаменника дробу на однакове число – рівноцінні дії, але в одних задачах доцільно помножити, в інших – поділити чисельник і знаменник дробу на одне й те саме число. Про це ми й поговоримо пізніше.
III. Відпрацювання навичок
І рівень
Усні вправи
1. Обгрунтуйте рівності: 
; 
; 
.
2. Чи правильні рівності: 
; 
; 
; 
? Відповідь обгрунтуйте.
3. Назвіть кілька дробів, що дорівнюють дробу 
.
ІІ, III рівні
Письмові вправи
1. Помножте чисельник і знаменник кожного дробу на 4 та запишіть відповідні рівності: 
; ; 
; 
; 
; 
.
2. Поділіть чисельник і знаменник кожного дробу на 5 та запишіть відповідні рівності: 
; 
; 
; 
; 
; 
.
3. Запишіть чотири дроби, що дорівнюють дробу 
, знаменники яких менші від знаменника даного дробу.
4. Замінить дроби 
; ; 
; 
; 
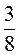дробами зі знаменником 48.
5. Поділіть чисельник і знаменник дробу 
на НСД чисельника і знаменника та запишіть відповідну рівність.
6. Накресліть відрізок завдовжки 4 см. Знайдіть у міліметрах довжини цього відрізка; 
його довжини. Зробіть висновок.
7. Зобразіть на числовому промені числа: 
; 
; 
; 
; 
; 
.
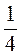8. Скільки міститься: а) десятих в ; б) дев’ятих в ; в) двадцятих у 
; г) шостих у 
; д) сотих в 
; є) четвертих у 
?
@ Хотілося б розв’язати на цьому уроці якомога більше вправ, що передбачають застосування основної властивості дробу як для множення, так і для ділення. Тому можна на основі запропонованих вправ скласти комплексні завдання, наприклад такі:
1. Запишіть дріб 
.
А) Помножте його чисельник і знаменник на 7 і запишіть відповідну рівність;
Б) поділіть його чисельник і знаменник на 2 і запишіть відповідну рівність;
В) запишіть три дроби, що дорівнюють даному з меншим знаменником;
Г) запишіть три дроби, що дорівнюють даному з більшим знаменником;
Д) запишіть його дробом зі знаменником 96;
Є) поділіть його чисельник і знаменник на НСД чисельника і знаменника;
Ж) скільки десятих, дванадцятих міститься у дробі, що ми його отримали в п. є)?
Запишіть це у вигляді рівнянь.
Замініть х таким числом, щоб була правильною рівність:
А) 
; б) 
; в) 
; г) 
; д) 
; е) 
.
Це опорна задача, її доцільно розібрати окремо після виконання пункту ж).
Доведіть, що дроби 
; 
; 
дорівнюють один одному.
Для сильних учнів можна запропонувати згадати ознаки подільності на 101 і 10001.
IV. Підсумки уроку
Як формулюється основна властивість звичайного дробу?
Чи правильний запис: 
; 
; 
?
V. Домашнє завдання
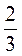1. Помножте чисельники і знаменники дробів 
; 
; 
на 6, а чисельники і знаменники дробів 
; 
; 
поділіть на 6. Запишіть відповідні рівності.
2. Запишіть три дроби, що дорівнюють дробу .
3. Замініть дроби ; 
; 
; 
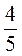; дробами зі знаменником 50.
4. Замініть х таким числом, щоб була правильною рівність: а) 
; б) 
; в) 
; г) 
.
5. Виразіть у копійках: від 3 грн; від 3 грн. Результати порівняйте.
6. Знайдіть НСД чисельника і знаменника дробу: а) 
; б) 
.
Повторіть алгоритм знаходження НСД і НСК.
(2 votes, average: 3,50 out of 5)