УРОК 59
Тема. Розв’язування систем логарифмічних рівнянь
Мета уроку. Формування умінь учнів розв’язувати системи логарифмічних рівнянь.
І. Перевірка домашнього завдання
Проводиться колективне обговорення виконання домашніх вправ за записами розв’язання вправ № 52 (9; 11), 53 (12), 54 (2; 7), підготовленими до початку уроку.
II. Самостійна робота
Варіант 1
Розв’яжіть рівняння:
А) lg(x2 – 2х) = lg(2x + 12). (3 бали)
Б) хlgх = 10. (3 бали)
В) log4 x + 3log4 x = 7. (3 бали)
Г) log2 (x2 + 4x + 1) + 1 = log2(6x + 2). (3 бали)
Варіант 2
Розв’язати
А) lg(2×2 + 3х) = lg(6x + 2). (3 бали)
Б) xlgx = 10 000. (3 бали)
В) log9 x + 2log9x = 5. (3 бали)
Г) log2 (x2 – 3) + 1 = log2(6x – 10). (3 бали)
Відповіді: В-1. а) 6; -2; б) 10; 0,1; в) 4; г) 0.
В-2. а) 2; б) 100; 0,01; в) 9; г) 2.
III. Розв’язування систем логарифмічних рівнянь
При розв’язуванні систем логарифмічних рівнянь використовують ті саме способи, що й при розв’язуванні алгебраїчних систем. Розглянемо приклади.
Приклад 1. Розв’яжіть систему рівнянь: 
Додамо і віднімемо почленно рівняння системи, тоді одержимо:
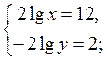
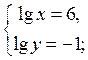

Відповідь: (106; 10-1).
Приклад 2. Розв’яжіть систему рівнянь 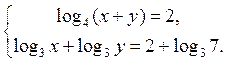








Тоді маємо  або
або  .
.
Перевіркою впевнюємося, що (9; 7), (7; 9) – розв’язки системи.
Відповідь: (9; 7), (7; 9).
IV. Формування умінь розв’язувати системи логарифмічних рівнянь
Розв’язування вправ № 55 (3; 4), 56 (2; 4), 57 (2).
V. Підведення підсумків уроку
VI. Домашнє завдання
Розділ V § 3. Запитання і завдання для повторення розділу V № 32. Вправи № 55 (1; 2), 56 (1, 3). Повторити властивості логарифмічної функції.
