Тема. Множення на розрядні числа. Повторення переставного та сполучного законів множення. Зображення круглого числа у вигляді добутку двох чисел, одним із множників якого є число 10, 100, 1000. Розв’язування задач, що включають знаходження числа за його дробом (№№ 806-813).
Мета. Повторити з учнями переставний та сполучний закони множення; вчити використовувати їх для спрощення обчислень; закріплювати вміння учнів зображати круглі числа у вигляді добутку двох множників, один з яких 10, 100, 1000; вчити розв’язувати складені задачі, що включають
Обладнання. Таблиця “Множення круглих чисел”; схема задачі; завдання для опитування учнів.
Зміст уроку
І. Контроль, корекція та закріплення знань.
1. Перевірка домашнього завдання.
А) Пояснити розв’язання задачі № 804.
(Розв’язання:
1) 2940 : 7 • 3 = 1260 (р.) – у 1-ому цеху;
2) 2940 – 1260 = 1680 (р.) – у 2-ому і 3-ому цехах;
3) 1680 : 2 = 840 (р.) – у 3-ому цеху.)
Б) Зачитати відповідь до задачі № 805.
(Відповідь: швидкість другого човна 28 км/год.)
2. Усні обчислення.
А) Знайти  від 21 (= 6); у від 40 (= 16);
від 21 (= 6); у від 40 (= 16); 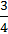
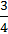 ц (= 75 кг);
ц (= 75 кг);  год (= 24хв);
год (= 24хв);  доби (= 16 год);
доби (= 16 год);  кг (= 300 г);
кг (= 300 г);  м (= 60 см).
м (= 60 см).Б) Задача.
Учень прочитав 50 сторінок, що становило  всієї книжки. Скільки сторінок у книжці? (Відповідь: 200 сторінок.)
всієї книжки. Скільки сторінок у книжці? (Відповідь: 200 сторінок.)
В)* У хлопчика запитали: “Яка твоя маса?” Він відповів жартома: “ ц ще
ц ще  моєї маси”. Яка маса хлопчика?
моєї маси”. Яка маса хлопчика?

Маса хлопчика становить 5 таких частин, по 5 кг кожна. (Маса: 25 кг.)
3. Завдання для опитування учнів.
А) 5 дівчаток зібрали 4 кг полуниць. Скільки полуниць одержала кожна дівчинка? (800 г)
Б) У трьох цехах приватного підприємства працює 352 робітники,  усіх робітників працює в першому цеху, а решта – у другому і третьому, порівну в кожному. Скільки робітників працює в третьому цеху? (66)
усіх робітників працює в першому цеху, а решта – у другому і третьому, порівну в кожному. Скільки робітників працює в третьому цеху? (66)
ІІ. Повторення законів множення.
1. Виконання завдання № 806 (1, 2) (усно).
2. Обчислення виразів зручним способом (№ 806 (3).)
8 • (5 • 3) = (8 • 5) • 3 = 40 • 3 = 120;
5 • 7 • 2 • 9 = (5 • 2) • (7 • 9) = 10 • 63 = 630;
(49 • 25) • 4 = (25 • 4) • 49 = 100 • 49 = 4900.
III. Множення на розрядні числа.
1. Виконання завдання № 808 (усно).
2. Запис розрядних чисел у вигляді добутку.
А) Вправа № 808 (1) (усно).
Б) Вправа № 808 (2) (письмово).
Фізкультхвилинка.
IV. Розвиток математичних знань.
1. Робота над задачами.
А) Задача № 809 (усно).
Б) Задача № 810 (фронтально).
Учні пояснюють, що 25 л – це тільки частина води, що була в бочці. Отже, води в бочці було 25 • 4 = 100 (л). Хлопчик витратив із 100 л 25 л на поливання огірків і 30 л на поливання яблунь. Всього він витратив 25 + 30 = 55 (л). Води в бочці залишилося 100 – 55 = 45 (л).
В) Задача № 811.

Відповідь на перше питання.
1) 12 • 10 = 240 (км) – пролетів літак за 20 хв;
2) 2 • 20 = 40 (км) – пролетів вертоліт за 20 хв;
3) 400 + 40 – 240 = 200 (км) – відстань між вертольотом і літаком через 20 хв.
(II варіант 3-ої дії: 400 – 240 + 40 = 200 (км).)
Відповідь на друге запитання.
Якщо через 20 хв відстань між літаком і вертольотом зменшилася у 2 рази (400 : 200 = 2 (рази), то ще через 20 хв вона становитиме 0 км, тобто літак порівняється з вертольотом через 40 хв (20 + 20 = 40 (хв).
Відповідь на третє запитання.
1 год = 60 хв
1) 12 • 60 = 720 (км) – пролетить літак за 1 год;
2) 2 • 60 = 120 (км) – пролетить вертоліт за 1 год;

3) 720 – 400 – 120 = 200 (км) – відстань між літаком і вертольотом через 1 год:
(II варіант 3-ої дії: 720 – (400 + 120) = 200 (км).)
Або методом міркування:
Якщо через 20 хв відстань між літаком і вертольотом становила 200 км, ще через 20 хв літак порівнявся з вертольотом (відстань між ними стала 0 км), то через наступні 20 хв (1 год – 20 хв + 20 хв + 20 хв) літак випередить вертоліт – знову ж таки, на 200 км.
2. Знаходження значень виразів.
(5194 – b) + b • 4 b = 985;
(а • 3) – (859 + а) а = 573.
А) Якщо b = 985, то (5194 – b) + b • 4 = (5194 – 985) + 985 • 4 = 8149.
Б) Якщо а = 573, то (а • 3) – (859 + а) = (573 • 3) – (859 + 573) = 287.
V. Підсумок уроку.
– Обчисліть вирази, використовуючи переставний і сполучний закони множення.
(47 • 25) • 4 = (25 • 4) • 47 = 100 • 47 = 4700:
89 • 2 • 5 = 89 • (2 • 5) = 89 • 10 = 890.
VI. Домашнє завдання.
№№ 812, 813 (с. 133).

