Урок № 88
Тема. Розподільна властивість множення. Зведення подібних доданків
Мета: завершити роботу з відпрацювання навичок використання розподільної властивості множення для: а) обчислень; б) розкриття дужок; в) зведення подібних доданків; г) винесення найбільшого спільного множника за дужки.
Тип уроку: застосування знань, умінь та навичок.
Хід уроку
I. Перевірка домашнього завдання
Усні вправи
1. Обчисліть, використовуючи розподільну властивість множення:
А) 4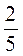
– 5; б) 2
; г) -18,6 – 8
+ 1
– (-18,6); д) 5,27 – (-15) – (-15) – (-4,73); є) 5
– 
– – .2. Спростіть вираз: а) 31а + 14а; б) 34х + 15х; в) 29b – b; г) 45у – у; д) х + 34х; е) а + 23а; ж) 2а – 3b + а.
II. Відтворення знань
Запитання до класу
1. Які доданки називають подібними?
2. Чим можуть відрізнятися один від одного подібні доданки?
3. Що означає “звести подібні доданки”? Як звести подібні доданки?
4. Які
ІІІ. Відпрацювання навичок
@ На ньому, третьому в темі “Розподільна властивість множення” уроці, ми завершуємо роботу з відпрацювання навичок застосування розподільної властивості множення для спрощення обчислень значень числових виразів та спрощення буквених виразів та винесення спільного множника за дужки. Також у кінці уроку пропонуємо самостійну роботу.
1. Розв’яжіть рівняння:
А) 3х + 2 – х = 6;
Б) 3(х – 1) – х = 0;
В) 7 – 3у + 4у – 4 = -1.
2. Винесіть за дужки спільний множник:
А) 7х + 7у;
Б) 15х – 10у;
В) 10m – mk;
Г) 16a + 8ab;
Д) 4ab + 6ac;
Є) 3mа – 6mb – 6mс.
3. Винесіть за дужки спільний множник:
a) 54xy – 62xz;
Б) 10ab – 15bc – 25b;
В) 42ах – 70ay – 84az.
4. Обчисліть найзручнішим способом:
А) -0,2 – 3,8 – 3, 7 – (-0,2);
Б) 
.
5. Спростіть вираз, використовуючи розподільну властивість множення:
А) 2(х – 7у + 3z);
Б) –
Х + 
Х – 
Х – х + с;
В) 0,6(4х – 12) – 0,4(5х – 7).
IV. Діагностика рівня засвоєння навчального матеріалу Тестові завдання
Варіант 1
1. Який результат дістанемо, застосувавши розподільний закон множення для обчислення виразу (0,03 + 2,5) – 0,4?
1) 1,12; 2) 10,12; 3) 1,012; 4) 2,12.
2. Який вираз дістанемо, розкривши дужки в добутку -5р(-х + 2у – 3k)?
1) -5хр + 10ру – 15рк;
2) 5рх – 10ру +15рк;
3) 5рх – 10рх – 15рк;
4) 5рх -2ру + 15рк.
3. Який вираз дістанемо, спростивши вираз 4с(3а – 2) – 6а(2с + 1)?
1) 12aс – 8с + 12ас + 6a; 2) -8с – 6а; 3) -8с + 6a; 4) 8с – 6а.
4. Обчисліть значення виразу 5-(5p – 4х) – 4-(х – 2p), якщо p = -2; х = 2.
1) -18; 2) -114; 3) -90; 4) 90.
5. Укажіть корінь рівняння -5-(у – 2) + 3(2 – у) = 0:
1) 8; 2) -2; 3) 2; 4) -0,25.
Варіант 2
1. Яке з поданих чисел дістанемо, застосувавши розподільний закон множення до виразу (12,5 + 0,1) – 0,8?
1) 100,8; 2) 18; 3) 10,8; 4) 10,08.
2. Який вираз дістанемо, розкривши дужки в добутку -2k(3а – 5b – 2с)?
1) 6ak – 10bk – 4ck;
2) 6ак +10bk + 4ck;
3) -6ak + 10bk + 4ck;
4) -3аk – 5bk – 4сk.
3. Який вираз дістанемо, спростивши вираз 5p – (-3 + k) – k – (5p – 1)?
1) -15p – k; 2) 15р – k; 3) -15р + k; 4) -15р + 5рk + 5рk – k.
4. Обчисліть значення виразу (2х – 3у) – 2-(5х – 2у), якщо х = -1, у = 1?
1) -9; 2) 1; 3) 9; 4) -1.
5. Знайдіть корінь рівняння (х – 1) – 2(1 – х) = 12:
1) 3; 2) 9; 3) 5; 4) -3.
IV. Підбиваємо підсумки уроку, перевіряючи якість виконання завдань тестової роботи
V. Домашнє завдання
1. Розв’яжіть рівняння: а) 7х – 3 – 6х + 3 = -5, б) 4(х – 5) – 3х + 6 = -2.
2. Спростіть вираз і знайдіть його значення:
А) -5(с + 2) – (2с – 3), якщо с = 1,5;
Б) 4х – 3а – 5х + 4а, якщо а = -0,27, х = 0,07.
3. Спростіть вираз: а) 1
А – А – а; б) 
B + 
B – 
B; в) (2х – у – 3) – (-2) – 2(2х – у); г) 2x(-3b + 5c) – x(2a – 4b).
4. Знайдіть добуток цілих розв’язків нерівності: а) -7 ? х? -1; б) -3 ? х < 2; в) -7 ? х < -1.
(1 votes, average: 5,00 out of 5)