УРОК № 8
Тема. Розв’язування задач на застосування теореми синусів
Мета уроку: формування вмінь учнів застосовувати теорему синусів до розв’язування задач.
Тип уроку: комбінований.
Наочність і обладнання: таблиця “Співвідношення між сторонами і кутами трикутника” [13], посібник [14].
Вимоги до рівня підготовки учнів: застосовують теорему синусів до розв’язування задач.
Хід уроку
І. Перевірка домашнього завдання
1. Фронтальне опитування
1) Сформулюйте теорему синусів. 2) У трикутнику ABC (рис.
А) 
;
Б) 
;
В) a2 = b2 + c2 – 2bcsin?;
Г) b = 2Rsin?.
3) У трикутнику ABC відомо, що 
A = 60°, B = 45°. Радіус кола, описаного навколо цього трикутника, дорівнює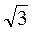 
см. Які з наведених тверджень є правильними, а які – неправильними?
А) ВС = 2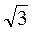SinB см;
Б) АС = 
см;
В) ВС = 3 см;
Г) АВ =
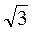Sin70° см.2. Перевірити правильність виконання домашніх вправ за записами, зробленими на дошці до початку уроку.
Розв’язання задачі
А) 
; 
; ? 
21°;
? = 180° – ? – ? 180° – 120° – 21° = 39o;
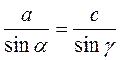; c = 
.
Відповідь, ? 21°, ? 39°, с 8,7.
Б) ; 
; ? 6°;
? = 180° – ? – ? 180° – 164° – 6° = 10°;
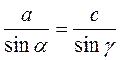; с = 
.
Відповідь. ? 6°, ? 10°, с 21,4.
II. Розв’язування задач
Використовуючи теорему синусів, доведіть, що:
А) у трикутнику проти більшого кута лежить більша сторона;
Б) проти більшої сторони лежить більший кут.
Наводимо зразок оформлення доведення теореми.
А) Дано: 0° < ? < 90°, 0° < ? < 90°, ? > ? (рис. 30). Довести, що а > b.
Доведення
Оскільки? > ?, то sin? > sin?. Ураховуючи, що 
, маємо: а > b.
Б) Дано: 90° < ? < 180° (рис. 31). Довести, що а > b.
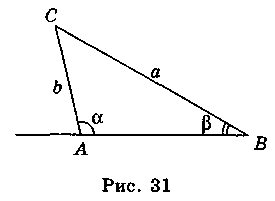
Доведення
Оскільки 90° < ? < 180°, то 0° < 180° – ? < 90°, 180° – ? > ? (як зовнішній кут трикутника, не суміжний з кутом?. Тому sin? = sin(180°- ?) > sin?. Ураховуючи, що , маємо: а > b.
В) Дано: а > b. Довести, що? > ?.
Доведення
Припустимо, що? < ?. Якщо? = ?, то а = b, що суперечить умові а > b. Якщо? < ?, то а < b, що суперечить умові а > b. Отже, припущення неправильне, тоді? > ?.
Усне розв’язування задач
1) У трикутнику ABC A = 32°, B = 63°. Яка зі сторін трикутника є:
А) найбільшою; б) найменшою?
2) У прямокутному трикутнику ABC (C = 90°) B = 18°. Який із катетів трикутника є:
А) більшим; б) меншим?
3) У трикутнику ABC АВ = 5 м, ВС = 6 м, АС = 7 м. Який із кутів трикутника є:
А) найбільшим; б) найменшим?
4) У трикутнику ABC АВ = АС = 10 см, ВС = 12 см. Які кути трикутника рівні? Який кут цього трикутника є найбільшим?
Колективне розв’язування задач
1) Доведіть, що коли в трикутнику є тупий кут, то протилежна йому сторона є найбільшою. 2) Що більше: основа чи бічна сторона рівнобедреного трикутника, якщо прилеглий до основи кут більший від 60°?
Розв’язання
Нехай АС = ВС (рис. 32), CAB > 60°, тоді CBA > 60°, АСВ = 180° – (CAB + CBA) < 60°. Оскільки ACB < CAB = CBA, то АВ < СА = СВ, тобто бічна сторона більша від основи.
Відповідь. Більшою є бічна сторона.
3) У трикутнику ABC кут С тупий. Доведіть, що коли точка X лежить на стороні АС, то ВХ < АВ.
Доведення
Якщо в трикутнику ABC (рис. 33) кут С тупий, то кут А є гострим.
AXB > ACB (за властивістю зовнішнього кута трикутника). Тоді в трикутнику AXB маємо: AXB > XAB, отже, АВ > ВХ, що і треба було довести.
4) У трикутнику ABC кут С тупий. Доведіть, що коли точка X лежить на стороні АС, а точка Y – на стороні ВС, то XY < АВ.
Доведення
Згідно з результатами задачі 3, із трикутника ABC (рис. 34) маємо ХВ < АВ. (1)
Із трикутника ХСВ (кут С тупий) аналогічно знаходимо: XY < XB. (2)
Ураховуючи нерівності (1) і (2), одержуємо: XY < ХВ < АВ. Отже, XY < АВ, що і треба було довести.
ІІІ. Самостійна робота
Самостійну роботу навчального характеру можна провести, скориставшись посібником [14], тест 3 “Теорема синусів та її наслідки”.
IV. Домашнє завдання
Розв’язати задачі.
1. У трикутнику ABC A = 40°, В = 60°, C = 80°. Яка із сторін трикутника є найбільшою, яка – найменшою? 2. У трикутнику ABC сторони АВ = 5,1 м, ВС = 6,2 м, АС = 7,3 м. Який із кутів трикутника є найбільшим, який – найменшим? 3. На стороні АВ трикутника ABC позначено точку D. Доведіть, що відрізок CD менший за одну із сторін: АС або ВС.
V. Підбиття підсумків уроку
Завдання класу
1. Сформулюйте теорему про співвідношення між кутами трикутника і протилежними сторонами. 2. У трикутнику дві сторони дорівнюють 3 см і 4 см. Чи може кут, протилежний стороні 3 см, бути тупим?
(1 votes, average: 5,00 out of 5)