Урок № 6 5
Тема. Цілі числа, раціональні числа
Мета: узагальнити і систематизувати відомості учнів про види чисел; домогтися засвоєння поняття “ціле число”, “раціональне число” і зв’язок між ними; навчити класифікувати числа.
Тип уроку: узагальнення і систематизація знань.
Хід уроку
І. Перевірка домашнього завдання (вибірково у “слабких” перевіряємо зошити)
Математичний диктант
Варіант 1 [2]
1. Напишіть число, протилежне числу 7 [самому собі].
2. Напишіть число, протилежне нулю [числу
3. Знайдіть число, протилежне числу -2 [4]. Запишіть відповідну рівність.
4. Запис – а [-(-b)] читають так…
5. Накресліть координатну пряму і побудуйте на ній число -5 [-4] і число, протилежне йому.
6. Знайдіть значення виразу – х, якщо х = – 4,2 [- у, якщо у = – 2,3].
7. * Чи існують 2 числа, які були б одночасно протилежними і взаємно оберненими? Чому?
II. Актуалізація опорних знань
Усні вправи
1. Обчисліть: а) 0,5 – 
; б) 3
– (0,6+0,4); в) 3,15 – 
; г) 
.
2. Назвіть перші 5 натуральних чисел і числа,
3. Назвіть: а) найбільше трицифрове натуральне число; б) найменше чотирицифрове натуральне число; в) число, що йде за найменшим трицифровим числом у натуральному ряді; г) число, що передує найменшому трицифровому числу в натуральному ряді. Знайдіть відповідні їм протилежні числа.
4. Які з названих чисел є: а) натуральними; б) звичайними дробами; в) мішаними числами; г) десятковими дробами?
0; 1; -1;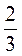 
; 2,5; 2; –
; -7,5; -3
.
Які числа залишились неназваними?
III. Узагальнення і систематизація знань учнів
1. Мотивація навчальної діяльності
@ Виконавши завдання 4 усних вправ, учні, по-перше, повторюють назви відомих їм типів чисел, а також доходять висновку, що є числа, які вони поки що не можуть віднести до жодного відомого їм класу чисел. Зрозуміло, що на уроці якраз і піде мова про це та про відношення між відомими учням класами чисел.
2. Узагальнення і систематизація, доповнення знань
А) Формуємо уявлення про цілі від’ємні числа як числа, протилежні до натуральних. Даємо означення цілого числа.
Б) Даємо узагальнену схему класифікації чисел, вводимо поняття раціонального числа.
Результатом бесіди можуть бути записи – на дошці і в зошитах учнів конспект 29.
@ 1. Важливо звернути увагу учнів на той момент, що будь-яке з чисел, шо ми можемо дістати, виконуючи арифметичні дії, є раціональним, але при цьому може бути натуральним, або цілим, або дробовим (на інтуїтивному рівні пояснюємо співвідношення множин та її підмножин).
2. Можливо, хтось з учнів зацікавиться питанням, чи існують інші, окрім раціональних, види чисел. Тому, в разі потреби, вчитель може повідомити учням, що є ще інші види дій з числами, а тому й інші види чисел. До речі, можна також показати учням, що ділення чисел на названі вище класи не є формальним, а пов’язане саме з арифметичними діями, які виконуються на кожному з названих класів (множин) чисел.
IV. Відпрацювання навичок
Усні вправи
1. Які з чисел 3; -17; 
; 0,7; 2,4; -1001; -3; 
:
А) цілі; б) дробові; в) раціональні?
2. Яке з тверджень є правильним?
А) Кожне натуральне число є цілим числом;
Б) кожне натуральне число є раціональним числом;
В) кожне ціле число є раціональним числом;
Г) якщо раціональне число не ціле, то воно дробове;
Д) якщо раціональне число не дробове, то воно ціле.
Письмові вправи
1. Напишіть 5 цілих чисел, які не є натуральними.
2. Скільки точок з цілими координатами є на координатній прямій:
а) ліворуч від точки О(0);
Б) праворуч від точки Л/(і 000);
В) між точками А (-4) і В (5)?
3. Які цілі числа розташовані на координатній прямій між числами:
А) -8 та -5; б) -3 та 0; в) -2 та 2; г) -3,6 та 4,2; д) –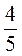
та 3; є) 2 та 5
; ж) -7
та -4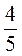; з) -11 та -3
?
4. Назвіть:
А) цілі числа, розташовані між числами -2 і 3;
Б) натуральні числа, розташовані між числами -2 та 3;
В) цілі від’ємні числа, розташовані між -2 і 3.
Додатково. Вправи на повторення
5. Запишіть числа:
А) обернені даним: 12; 
; 2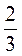; 0,6;
Б) протилежні до даних: 12; ; -2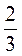; 0,6; -8,6; -2
; 0;
В) обернені даним і протилежні до даних: 8; 2,6; 
.
Дані й утворені числа зобразити точками на координатній прямій.
6. Назвіть числа, протилежні й обернені до значення виразу:
А) 5,2 – 2,4 + 5,2 – 5,6; б) 
; в) 
; г) 
.
7. Задача. Вітя купив 2,4 кг моркви. Скільки моркви купив Микола, якщо він купив:
А) на 0,7 кг більше за Вітю;
Б) на 0,9 кг менше від Віті;
В) в 3 рази більше за Вітю;
Г) в 1,2 раза менше від Віті;
Д)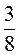 
того, що купив Вітя;
Є) 
того, що купив Вітя;
Ж) 0,5 того, що купив Вітя;
З) 20 % того, що купив Вітя;
К) 120 % того, що купив Вітя;
Л) на 20 % більше того, що купив Вітя?
V. Підсумок уроку
Які з чисел -83; 
; -2; –
– цілі; дробові; натуральні; раціональні?
Закінчіть речення:
А) Число, протилежне до натурального, є…
Б) Число, обернене до натурального, є…
VI. Домашнє завдання
1. Дано числа: 1; 29; -3,7; 4,3; –
; 0; 4,9; –
; 18; -11. Випишіть з них: а) натуральні; б) цілі; в) дробові; г) додатні; д) від’ємні.
2. За нормами площа всіх вікон повинна становити площі підлоги класної кімнати. Визначте, чи достатньо світла у класі, довжина якого 8,5 м, а ширина на 2 м менша від довжини, якщо в ньому 3 вікна висотою 2 м і шириною 1,5 м.
3. Виконайте дії і знайдіть числа, протилежні і обернені до значень виразів:
А) 
; б) 
.
(1 votes, average: 5,00 out of 5)