Математика – Алгебра
Степенева функція
Ірраціональні рівняння
Рівняння, в яких невідоме міститься під знаком кореня, називають Ірраціональними. Розв’язуючи ірраціональні рівняння, намагаються привести їх до вигляду:
, або 
, а потім піднести обидві частини рівняння до n-го степеня. Але якщо піднести обидві частини рівняння до парного степеня, можуть з’явитися сторонні корені. Нариклад:
, ОДЗ: 
;
,
, 
.
; 
– правильно.Але якщо
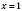, маємо 
;
, тобто 
– сторонній корінь.Доцільно розв’язувати ірраціональні рівняння одним із двох наведених способів.
І спосіб
Виконувати перетворення, не зважаючи на їх рівносильність. Усі одержані корені перевірити. Зверніть увагу: для перевірки корінь треба підставляти
При цьому способі розв’язання доцільно записати, при яких значеннях невідомого обидві частини рівняння мають зміст. Іноді в процесі розв’язування отримують сторонні корені, які не задовольняють ОДЗ. Але перевірка коренів за умовами ОДЗ не є достатньою. У наведеному вище прикладі сторонній корінь 1 задовольняє ОДЗ
.II спосіб
Можна розв’язувати ірраціональні рівняння, використовуючи тільки рівносильні переходи. Зручно користуватися такими твердженнями:
1)
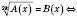
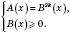
2)
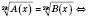
Приклади
1)
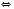
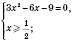
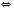
.2)
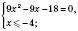
Розглянемо ще декілька прикладів розв’язування ірраціональних рівнянь.
1. Відокремлювання кореня
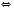
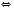
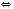
2. Ірраціональні рівняння, що зводяться до квадратних
Якщо рівняння містить вирази
і 
, то можна використати, що 
для тих значень х, при яких 
.Отже, введемо нову змінну
. Дістанемо 
.Приклад
, ОДЗ: 
.Нехай
, 
.
,
, 
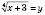не задовольняє умову 
.
,
; 
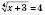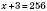.Відповідь: 253.
3. Заміна змінної.
Приклад
,ОДЗ:
.Нехай
, 
.Тоді
.Отже,
,
,
,
, 
не задовольняє умову 
.
,
,
.
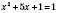Відповідь: 0; –5.
4. Рівняння виду
Скористаємось тотожністю
.Приклад
.Піднесемо обидві частини рівняння до третього степеня:
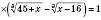.Треба знайти такі значення х, для яких
. Отже, маємо:
,
,
,
,
,
Цей спосіб розв’язання потребує перевірки.
Перевірка
.
;
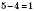– правильно.
.
;
– правильно.Відповідь: 80; –109.
(1 votes, average: 5,00 out of 5)