Урок № 58
Тема. Круговий сектор
Мета: сформувати уявлення про повний кут, круговий сектор і вимірювання секторів частинами повного кута; відпрацювати навички розв’язування задач на застосування формул C = nD, S = nR2 та поняття кругового сектора.
Тип уроку: засвоєння вмінь та навичок.
Хід уроку
І. Перевірка домашнього завдання
@ Вибірково (у “слабких” учнів на перерві перевіряємо якість виконання домашнього завдання) на уроці фронтально перевіряємо виконання домашніх задач 2, 3. Засвоєння формули S = nR2 і навичок
1. Напишіть формулу, за якою обчислюється площа круга, якщо відомо радіус кола.
2. Округліть число n до сотих і запишіть результат.
3. Обчисліть площу круга, довжина радіуса якого 3 дм, округливши n до сотих.
4. Обчисліть площу фігури, зображеної на рисунку, взявши число n у вигляді неправильного дробу.
II. Актуалізація опорних знань
Ігровий момент
Закінчіть речення:
Фігура, що складається з кола і частини площини, що знаходиться всередині кола, називається…
Відрізок, що сполучає
Фігура, що складається з точки і двох променів, що виходять з цієї точки, називається…
Кут вимірюється у…
Найбільший з кутів… Його градусна міра…
ІІІ. Формування знань
1. Поняття кругового сектора
Конструктивно формуємо уявлення про сектор: Круг з центром в т. О і радіусом О А і О В ділиться на дві частини: один і два – кругові сектори.
@ Автор вважає, що не треба від учнів вимагати знання означення сектора (як частини круга, що обмежена двома радіусами), але вміти зображувати і знаходити на готових рисунках ці фігури обов’язково.
2. Як вимірюються кругові сектори?
А) Градусною мірою кута, що утворюють радіуси;
Б) можна знаходити площу сектора.
3. Чому дорівнює сума градусних мір всіх секторів даного круга?
На рис. ОА і ОВ – радіуси, отже, маємо два сектори: перший і другий, але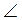 
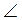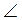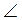1 = 180° і 2 = 180°, тому 1 + 2 = 360° повний кут.
Отже, запам’ятайте, повний кут – 360°. Скільки градусів становить круговий сектор, якщо він становить 
; 
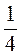; 5 % повного кута?
Підсумок
1. Сектор – це фігура, яка є частиною круга, обмежена двома радіусами круга.
2. Сектор характеризується:
А) градусною мірою кута, що утворюють його радіуси; б) площею.
IV. Застосування знань. Формування вмінь
Розв’язування вправ
@Основна мета – навчитися будувати сектори, якщо відомо, яку частину (виражену дробом або відсотками) сектор становить від повного кута, а також не забуваємо виконувати задачі на застосування формул C = nD i S = nR2.
Задача 1. Поділіть круг на сектори, кути яких становлять 15 %; 
; 0,2 повного кута відповідно. Обчисліть величину кута четвертого сектора.
Задача 2. Поділіть кут на сектори, якщо градусна міра одного з їх кутів на 20° більша за градусну міру другого і на 40° менша від градусної міри третього.
Задача 3. Дано круг із центром О і радіусом 12 см (рис). Знайдіть площу заштрихованого сектора, якщо 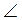AOB = 60°.
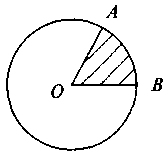
(Перед розв’язуванням цієї задачі можна запропонувати учням таке запитання:
Яку частину становить площа сектора від площі круга, якщо градусна міра круга сектора складає: а) 90°; б) 30°; в) 45°; г) 1°?)
Задача 4. Довжина діаметра кола 70 см. Скільки приблизно треба зробити обертів, щоб подолати відстань у 3 км?
Задача 5. Знайдіть площу заштрихованої фігури, виконавши необхідні обчислення:
А)
| Б) АВ = 4см
|
V. Підсумки уроку
Бліцтест
1. На якому з рисунків заштрихована фігура не є круговим сектором?
А)
Б)
В)
Г)
2. Знайдіть кут, яким вимірюється сектор 3 на рисунку.
А) 180°; б) 90°; в) 225°; г) 360°.
VI. Домашнє завдання
Задача 1. Накресліть коло радіуса 2,5 см. Проведіть радіус ОА, діаметр АВ, хорду ВС, заштрихуйте сектор АОС.
Задача 2. Довжина кола дорівнює 12,56 дм. Знайдіть площу круга, обмеженого цим колом.
Задача 3. Поділіть круг на сектори, кути яких становлять 
; 0,4; 25 % повного круга відповідно. Обчисліть величину кута четвертого сектора.
(2 votes, average: 3,00 out of 5)