Математика – Алгебра
Логарифмічна функція
Логарифмічні нерівності
Розв’язуючи логарифмічні нерівності, спираються на такі твердження.
1. Якщо 
, то нерівність 
рівносильна подвійній нерівності 
.
Це твердження можна записати у вигляді:
або 
2. Якщо 
, то
рівносильна подвійній нерівності 
.Це твердження можна записати у вигляді:
або
Зверніть увагу: при розв’язуванні логарифмічної нерівності немає сенсу окремо виписувати ОДЗ, оскільки все одно буде необхідно розв’язувати систему нерівностей, яка включає й ОДЗ.
Приклади
1)
.Логарифмічна функція
з основою 
спадна,
Відповідь:
(або у вигляді 
.2)
.Нехай
.
, 
, 
.
Відповідь:
або 
3)
.Розглянемо два випадки.
.
.Об’єднуючи ці проміжки, одержимо відповідь.
Відповідь:
.4)
.
; основою логарифма може бути тільки додатне число, яке не дорівнює 1. Виходячи з цього, отримуємо, що дана нерівність рівносильна системі: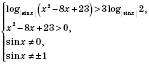
Якщо
, то 
; 
.Якщо
, то 
; 
.Відповідь:
.
(1 votes, average: 5,00 out of 5)Логарифмічні нерівності - Довідник з математики
Схожі записи:
Додавання і віднімання дробів з однаковими знаменниками Математика – Алгебра Звичайні дроби Додавання і віднімання дробів з однаковими знаменниками Щоб додати дроби з однаковими знаменниками, треба додати їх чисельники і суму записати...
Властивості функцій – Функції та графіки Математика – Алгебра Функції та графіки Властивості функцій Функція називається Зростаючою на деякому проміжку, якщо більшому значенню аргументу із цього проміжку відповідає більше значення функції....
Задачі на відсотки – Приклади розв’язування типових завдань Математика – Алгебра Приклади розв’язування типових завдань Задачі на відсотки Задачі на відсотки – це задачі на пряму пропорційність. Задача 1. Зі свіжих слив виходить...
Прості й складені числа Математика – Алгебра Подільність натуральних чисел Прості й складені числа Натуральне число називається Простим, якщо воно має тільки два різних дільники: одиницю й саме це...
Задачі на спільну роботу – Приклади розв’язування типових завдань Математика – Алгебра Приклади розв’язування типових завдань Задачі на спільну роботу У розв’язанні цих задач велику роль відіграють такі величини: частина всієї роботи, яку виконує...
Похідна Математика – Алгебра Похідна Похідною функції в точці називається границя відношення приросту функції до приросту аргументу за умови, що границя існує, а приріст аргументу прямує...
Звичайні дроби Математика – Алгебра Звичайні дроби Записи виду називаються звичайними дробами, або дробами. Звичайні дроби записують за допомогою двох натуральних чисел та горизонтальної риски, яка називається...
Графік лінійного рівняння з двома невідомими – Системи лінійних рівнянь Математика – Алгебра Системи лінійних рівнянь Графік лінійного рівняння з двома невідомими Графіком рівняння з двома невідомими називається множина всіх точок координатної площини, координати котрих...
Поняття первісної функції – Інтеграл і його застосування Математика – Алгебра Інтеграл і його застосування Поняття первісної функції Первісною для даної функції на заданому проміжку називається така функція , що для всіх ....
Числовий промінь Математика – Алгебра Числовий промінь Накреслимо промінь Оx горизонтально праворуч від точки О. Проти початку променя напишемо число 0. Відкладемо від 0 довільний відрізок, який...
Екстремуми функції Математика – Алгебра Числові функції Екстремуми функції Точку x0 називають Точкою мінімуму функції, а саме число – Мінімумом функції, якщо існує інтервал , , на...
Показникові рівняння Математика – Алгебра Степенева функція Показникові рівняння Показниковими рівняннями називають такі рівняння, в яких невідоме входить лише до показників степенів при сталих основах. Розв’язування показникових...
Властивості модуля – Модуль і його властивості Математика – Алгебра Модуль і його властивості Модуль числа – це відстань від 0 до точки, що відповідає цьому числу на координатній прямій, виміряна в...
Множення звичайних дробів Математика – Алгебра Множення і ділення звичайних дробів Множення звичайних дробів Добутком звичайних дробів є дріб, чисельник якого дорівнює добутку чисельників цих дробів, а знаменник...
Рівняння Математика – Алгебра Натуральні числа і дії над ними Рівняння Рівність, що містить невідоме число, називається Рівнянням. Значення невідомого, при якому рівняння перетворюється у правильну...
Кoрінь n-го степеня та його властивості Математика – Алгебра Степенева функція Кoрінь n-го степеня та його властивості Коренем N-го степеня з числаА називається таке число, n-й степінь якого дорівнює а. Якщо...
Задачі на рух – Приклади розв’язування типових завдань Математика – Алгебра Приклади розв’язування типових завдань Задачі на рух Задача. Відстань від А до В дорівнює 120 км. Відстань від А до В автомобіль...
Розв’язування квадратного рівняння – Виділення повного квадрата Математика – Алгебра Квадратні корені Виділення повного квадрата Розв’язування квадратного рівняння Способом виділення квадратного двочлена розглянемо на прикладі. . Розв’язання Поділимо всі коефіцієнти рівняння на...
Порівняння, додавання та віднімання дробів – Додавання і віднімання звичайних дробів Математика – Алгебра Додавання і віднімання звичайних дробів Порівняння, додавання та віднімання дробів Щоб виконати порівняння, додавання, віднімання дробів із різними знаменниками, треба звести їх...
Найбільший спільний дільник (нсд) Математика – Алгебра Подільність натуральних чисел Найбільший спільний дільник (нсд) Найбільше натуральне число, на яке ділиться кожне з чисел a і b, називається найбільшим спільним...
Лінійні рівняння з одним невідомим Математика – Алгебра Рівняння Лінійні рівняння з одним невідомим Рівняння виду , де a і b – деякі числа, а х – невідоме, називається Лінійним...
Основна властивість дробу. Скорочення дробів – Раціональні вирази Математика – Алгебра Раціональні вирази Основна властивість дробу. Скорочення дробів Якщо чисельник і знаменник дробу помножити або поділити на один і той самий вираз, то...
Основні теореми про границі числової послідовності Математика – Алгебра Границя Основні теореми про границі числової послідовності Теорема 1. Нехай послідовності і мають відповідно границі a і b. Тоді послідовність має границю...
Метод інтервалів Математика – Алгебра Границя Метод інтервалів Отже, нехай функція неперервна на інтервалі І й перетворюється на 0 у скінченній кількості точок цього інтервалу. Тоді інтервал...
Застосування кількох способів для розкладання многочленів на множники Математика – Алгебра Многочлен Застосування кількох способів для розкладання многочленів на множники Щоб розкласти многочлен на множники, бажано діяти в такій послідовності. 1. З’ясувати, чи...
Приклади функцій і їх графіків Математика – Алгебра Функції Приклади функцій і їх графіків Лінійна функція Лінійною називається функція, яку можна задати формулою , де х – аргумент, а k...
Послідовності Математика – Алгебра Послідовності Розглянемо яку-небудь множину, що містить дійсних чисел і кожний елемент якої відповідає одному з натуральних чисел від 1 до , або...
Степінь Математика – Алгебра Подільність натуральних чисел Степінь Добуток n однакових множників, кожний із яких дорівнює а, називається n-м Степенем числа А і записується : ,...
Знаки тригонометричних функцій Математика – Алгебра Тригонометричні функції Знаки тригонометричних функцій З означення тригонометричних функцій легко зробити висновок щодо знаків тригонометричних функцій у координатних чвертях: Зміна тригонометричних функцій...
Розв’язування рівнянь графічним способом Математика – Алгебра Функції Розв’язування рівнянь графічним способом За допомогою графіків функцій можна розв’язувати рівняння графічним способом. Для цього треба побудувати в одній системі координат...
Найменше спільне кратне Математика – Алгебра Подільність натуральних чисел Найменше спільне кратне Найменшим спільним кратним натуральних чисел a і b називається найменше натуральне число, яке ділиться на кожне...
Многокутник – Геометричні фігури й величини Математика – Алгебра Геометричні фігури й величини Многокутник На рисунку ABCDE – п’ятикутник. A, B, С, D, E – вершини п’ятикутника; AB, BC, CD, DE,...
Властивості десяткового дробу – Десяткові дроби Математика – Алгебра Десяткові дроби Властивості десяткового дробу Якщо до десяткового дробу дописати справа нуль (або декілька нулів), то дістанемо дріб, який дорівнює даному. Якщо...
Геометричні фігури й величини Математика – Алгебра Геометричні фігури й величини На рисунках, поданих нижче, наведені деякі основні геометричні фігури; поруч даються назви й позначення. Відрізок AB (або BA)....
Правила знаходження первісних – Інтеграл і його застосування Математика – Алгебра Інтеграл і його застосування Правила знаходження первісних 1. Якщо є первісною для , а – первісною для , то є первісною для....