Урок № 69
Тема. Порівняння раціональних чисел
Мета: відпрацювати навички порівняння раціональних чисел у комплексі із набутими раніше навичками (з теми про додатні і від’ємні числа).
Тип уроку: застосування знань, умінь і навичок.
Хід уроку
І. Перевірка домашнього завдання. Актуалізація опорних знань
А. Усні вправи (фронтальна робота із сигнальними картками або математичний диктант)
1. Закінчіть речення: “З двох чисел менше те, зображення якого розташоване на координатній прямій…”
2. Якщо х
3. Порівняйте:
А) 2 та -300; б) -7 та -9;
В) а та b; а та 0; b та 0, якщо а – додатне, b – від’ємне.
Б. Картки із завданнями (індивідуальна робота)
Картка 1 |
Розташуйте в порядку спадання числа: А) -6; 7; -7; 8; -8; 9; -9; 10; -10; б) -1; 0; 1; -0,01; 0,001; -0,0001; 0; В) 2,8; -2,7; 2,6; -2,08; 2,07; -2,06; 0. |
Картка 2 |
Порівняйте числа: А) |-0,3| та |-0,5|; б) |4,1| та |1,4|; в) |-6,5| та |5,9|; г) |-12,01| та |-1,09|; Д) |-8,1| та |6,2|; е) |0| та |-0,002|; ж) |17,2| та |-2,7|. |
В. Роботи учнів перевіряємо вибірково,
II. Застосування навичок
@ На цьому уроці розв’язуємо вправи більш високого рівня складності (узагальнюючі та дослідницькі) і повторюємо поняття додатного, від’ємного числа, “раціональні числа”, “модуль числа”.
1. Між якими сусідніми цілими числами стоїть число?
А) -2,73; б) -9,5; в) -0,63; г) 0,87; д) -1 ; є) -6
; є) -6 .
.
Відповідь запишіть у вигляді подвійної нерівності.
2. Які цифри можна записати замість *, щоб утворилася правильна нерівність:
А) -3841 < -384*; б) -*5,44 > -25,44; в) – < –
< – ; г) –
; г) – > –
> –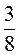 ?
?
3. Запишіть у вигляді нерівності речення:
А) -4,3 – від’ємне число;
Б) 27,1 – додатне число;
В) а – від’ємне число;
Г) b – додатне число;
Д) * с – невід’ємне число;
Є) * d – недодатне число.
4. Ігровий момент

Учень, якого викликали до дошки, називає і показує по черзі то “червоні”, то “сині” числа, записані в таблиці. При цьому “червоні” числа називає в порядку зростання, а “сині” – в порядку спадання, тобто називає числа в такій послідовності: -6; 2; -5; 0; -4; -1; -2; -3; 1.
Якщо учень помилився, то сідає на місце, і до дошки йде інший.
III. Діагностика засвоєння знань і вмінь
Самостійна робота
Варіант 1
1. Накресліть координатну пряму з одиничним відрізком 1 см. Позначте на координатній прямій:
А) точки A(2); B(-3,5); C(-1); D(-2); Е ; F(3);
; F(3);
Б) точку K і точку M, що має протилежну координату;
і точку M, що має протилежну координату;
В) точки, модулі координат яких дорівнюють 5; 4,5; 0.
2. Дано числа: 6; -9; 5,25; 2 ; 507; 9; -2,6; 1,125; 0; -207; -5
; 507; 9; -2,6; 1,125; 0; -207; -5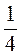 .
.
А) Які з даних чисел є: натуральними? цілими? дробовими? додатними? від’ємними?
Б) Знайдіть модулі цих чисел. Які з даних чисел мають рівні модулі? Чому?
В) Розмістіть числа в порядку зростання.
Варіант 2
1. Накресліть координатну пряму з одиничним відрізком 1,5 см (3 клітинки). Позначте на цій прямій:
А) точки M(2), N  , Р(-1), К(-2), R
, Р(-1), К(-2), R  , 5(3);
, 5(3);
Б) точку А  і точку В, що має протилежну координату;
і точку В, що має протилежну координату;
В) точки, модулі яких дорівнюють 4; 1 ; 0.
; 0.
2. Дано числа: 0; 7; -11; -3,8; 4 ; 239; 3
; 239; 3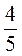 ; 11; -400; -4,4.
; 11; -400; -4,4.
А) Які з даних чисел є: натуральними? цілими? дробовими? від’ємними?
Б) Знайдіть модулі цих чисел. Які з них мають рівні модулі? Чому?
В) Розмістіть числа в порядку спадання.
IV. Підсумки уроку
Перевіряємо якість виконання самостійної роботи. Аналізуємо помилки.
V. Домашнє завдання
1. Порівняйте числа, а результат запишіть у вигляді нерівності:
А) – та
та  ; б) 3 та –
; б) 3 та –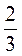 ; в) –
; в) – та –
та –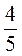 ; г) -2
; г) -2 та 3
та 3 ; д) –
; д) – та –
та –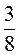 ; е) –
; е) – та –
та – ; ж) -2
; ж) -2 та -3
та -3 ; з) -5
; з) -5 та -5
та -5 .
.
2. Розташуйте числа 5; -9; 0; 0,88; -6,9; 8,92 у порядку спадання.
3. * Перевірте справедливість нерівностей
1) |a + b| ? |a| +|b|;
2) |a – b| ? |a| + |b|;
3) |a| – |b| ? |a + b|;
4) |a| – |b| ? |а – b|;
5) |а| – |b| ? |a| + |b|.
При таких значеннях букв:
А) а = -7; b = -5; б) а =  ; b =
; b = 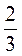 ; в) а = 4; b = -5.
; в) а = 4; b = -5.

 (2 votes, average: 4,00 out of 5)
(2 votes, average: 4,00 out of 5)