УРОК 44
Тема. Застосування властивостей показникової функції до розв’язування вправ
Мета уроку. Формування умінь учнів застосовувати властивості показникової функції до розв’язування вправ. Познайомити учнів з використанням показникової функції під час вивчення явищ навколишнього середовища.
І. Перевірка домашнього завдання
Колективне обговорення № 1-12 із “Запитання і завдання для повторення” § 1 розділу IV.
II. Набуття умінь застосовувати властивості показникової функції до розв’язування вправ
Початковий
1. Знайдіть значення функції у = 3х, якщо: а) х = 2; б) х = – 2; в) х = 0.
Відповідь: а) 9; б) 
; в) 1.
2. На якому з рисунків (рис. 144) подано графік функції: a) y =5х; б) 
?
Відповідь: а) І; б) IV.
3. Користуючись графіком функції у = 2х, порівняйте значення виразів (рис. 145): а) 210 і 220; б) 2-10 і 210; в) 2-10 і 2-20.
Відповідь: а) 210 < 220; б) 2-10 < 210; в) 2-10 > 2-20.
4. Користуючись графіком функції 
, порівняйте значення виразів (рис. 146): a)
і 
; б) 
І ; в) 
І .Відповідь: a) > ; б) > ; в) > .
Середній рівень
1. Знайдіть область визначення функцій: а) y = 2x + 6; б) 
; в) y = 3x + 1; г) 
.
Відповідь: a) R; б) R; в) R; г) R.
2. Побудуйте схематично графік функцій:
A) y = 1,7x; б) 
; в) y = 0,3х; г) 
.
Відповідь: рис. 147: а); б); в); г).
3. Порівняйте числа: а) 1,83 і 1; б) 0,85 і 1; в) 
і 5-4; г) 
і 
.
Відповідь: а) 1,83 > 1; б) 0,85 < 1; в) > 5-4; г) >.
4. Порівняйте числа х і у, якщо відомо, що вірна нерівність:
А) 
< 
; б) 
< 
; в) 3х < 
; г) 
<
.
Відповідь: а) х < у; б) х > у; в) х < у; г) х < у.
5. Порівняйте основу a > 0 з одиницею, якщо відомо, що вірна нерівність:
А) а-2 > а2; б) аn > а3; в) 
; г) 
.
Відповідь: а) 0 < a < 1; б) а > 1; в) 0 < а < 1; г) а > 1.
Достатній рівень
1. Знайдіть область визначення функцій: а) 
; б) y=
; в) 
.
Відповідь: а) R; б) [0; +
); в) (-; -1) 
(-1; 1) (1; +).
2. Побудуйте графіки функцій: a) y =3x + 1; б) 
; в) y = nх – 2; г) y = 3х+1.
Відповідь: (рис. 148) а); б); в); г).
Рис. 148
3. Знайдіть множину значень функцій:
А) у = -3х; б) 
; в) 
; г) y = 5х – 3.
Відповідь: а) (-; 0); б) (3; +); в) (-; 0); г) (-3; +).
4. Який висновок можна зробити відносно показника х, якщо:
А) 5х = 10; б) 5х = 3; в) 0,01х = 2; г) 100х = 2.
Відповідь: а) х > 1; б) 0 < х < 1; в) 0 < х < 1; г) 0 < х < 1.
Високий рівень
1. Знайдіть область визначення функцій:
А) 
; б) 
; в) 
; г) 
.
Відповідь: а) х? 
+ ?n, n
Z; б) х? + 2?n, nZ;
В) – + 2?n 
х + 2?n, nZ; г) ?n х < + ?n, nZ.
2. Побудуйте графіки функцій:
A) у =
; б) у = 
; в) 
; г) 
.
Відповідь: (рис. 149) а); б); в); г).
Рис. 149
3. Знайдіть найбільше і найменше значення функції:
А) 
; б) 
; в) y = nsinx; г) 
.
Відповідь: а) найбільшого немає, найменше 1; б) найбільше 2, найменше 1; в) найбільше n, найменше 
; г) найбільше 1, найменше 
– 1.
III. Сприймання і усвідомлення нового матеріалу
Показникова функція часто використовується для описання різних процесів у природі і техніці.
Так, радіоактивний розпад виражається формулою 
Де m(t) – маса радіоактивної речовини в момент часу t;
Т0 – маса радіоактивної речовини в момент часу t = 0;
Т – період напіврозпаду (проміжок часу, за який початкова кількість речовини зменшується удвічі).
За допомогою показникової функції виражається тиск повітря в залежності від висоти підйому, приріст деревини, кількість бактерій, які розмножуються в деякому середовищі тощо.
Більш детальніше про практичне використання показникової функції ви прочитаєте в підручнику. А зараз розв’яжемо задачу.
При радіоактивному розпаді кількість речовини зменшується вдвічі за добу. Скільки речовини залишиться від 250 г через: а) 1,5 доби; б) 3,5 доби?
За умовою задачі т0 = 250 г, Т = 1 доба. За законом радіоактивного розпаду маємо:
, 
.
Знайдемо m(1,5) і m(3,5):
А) 
= 250 – (0,5)1,5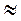 
88,4 (г);
Б) 
= 250 – (0,5)3,5 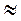22,1 (г).
IV. Підсумок уроку
V. Домашнє завдання
Розділ IV § 1. “Запитання і завдання для повторення” № 13-16, 25.
(2 votes, average: 3,50 out of 5)