Урок № 8 5
Тема. Коефіцієнт
Мета: використовуючи знання учнів про правила і властивості множення раціональних чисел, сформувати їх уявлення про спосіб перетворення добутку, що містить числові та буквені множники, зміст поняття “коефіцієнт” та виробити вміння обчислювати коефіцієнти буквених виразів.
Тип уроку: засвоєння нових знань.
Хід уроку
І. Перевірка домашнього завдання
@ Задля економії часу на уроці перевіряємо домашнє завдання у зошитах лише “слабких” учнів (перед уроком), а на уроці проводимо
II. Актуалізація опорних знань
Усні вправи
1. Обчисліть найбільш зручним способом:
А) (-2) – (-37) – (-5);
Б) (-25) – 106 – (-4);
В) -4 – (-0,81) – 25;
Г) 
.(-8) – 
;
Д) -2,5 – (-13,4) – 40;
Є) (-1,23) – (-4) – (-5) – (-5);
Ж) 
;
З) 5
– (-0,02) – 
Якими властивостями множення ви користувались?
2. Прочитайте записи. Що вони означають? 2а; – а; 3аb.
3. Використовуючи сполучну та переставну властивості множення, спростіть вираз:
A) 2a – 3b; б) 0,2a – 3b; в) 0,2а – 0,3b; г) 
А – B; д) 
-3b.
4. Замість * поставте таке число, щоб рівності були правильними: * а = а;* – а = – а; * 0 = 0.
III. Формування знань
Головною метою уроку (це і є змістом нового для учнів матеріалу) є поняття коефіцієнта буквеного виразу. (Із застосуванням сполучної та переставної властивості множення для спрощення буквених виразів учні знайомі ще з 5 класу). Тому розглянувши декілька типових прикладів, вводимо поняття “коефіцієнт буквеного виразу”, а також не забуваємо про особливі випадки (коли коефіцієнт дорівнює 1 або -1).
План викладення нового матеріалу
1. Поняття коефіцієнта
Єдиний числовий множник у добутку – це коефіцієнт. Приклад: -0,5а – коефіцієнт -0,5; -4ab – коефіцієнт -4.
@ Зазвичай коефіцієнт пишуть на першому місці в добутку.
2. Як знайти коефіцієнт буквеного виразу?
Якщо числовий множник – єдиний, то він і є коефіцієнтом – пишемо його на першому місці.
Якщо в добутку кілька числових множників, використовуємо сполучну та переставну властивості множення і спрощуємо вираз: єдиний числовий множник, що утвориться, буде коефіцієнтом.
Наприклад. У виразі -5b – 7с = (-5 – 7) – (b – с) = -35bс коефіцієнт -35.
3. Особливі випадки
Ви вже знаєте (див. усні вправи 4), що а – 1 = а, а – (-1) = – а, тому домовимося, що коефіцієнт 1 або -1 ми писати будемо не повністю, а саме запишемо тільки знак “+” або “-“.
Наприклад. У виразі abc – коефіцієнт 1, а у виразі – dce – коефіцієнт -1.
IV. Вироблення вмінь
Усні вправи
1. Назвіть коефіцієнт добутку: а) 7а;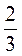 
B; -8с; –Х; 2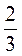У; -1,8m; б) – a; – b; х; y; – z; m; п.
2. Обчисліть коефіцієнт добутку: а) 5b – (-3с); б) а – (-b); в) – а – (-b); г) –А -(+2b).
Письмові вправи
@ На цьому уроці продовжується робота з відпрацювання навичок спрощення буквених виразів із застосуванням переставної та сполучної властивостей множення. До цього додається завдання виробити вміння знаходити коефіцієнт у буквеному виразі. Атому перед розв’язуванням письмових вправ ще раз звертаємося до плану (див. п. IIІ) і наголошуємо, що коефіцієнт буквеного виразу – це єдиний числовий множник у добутку, тому, перш ніж знайти коефіцієнт, обов’язково спростити вираз. Розв’язуємо вправи.
1. Спростіть вираз та знайдіть його коефіцієнт:
А) -7,2 – x – 10; б) 2,5 – a – (-4) – 6; в) -2,4 – х – (-3); г) -8 – 5 – a – (-2) – b; д) -5a – 
– 2; є) –
А – 
– 4b.
2. Спростіть вираз: а) -6,4 – 
– 
; б) 5,25 – x – 
–
; в) -0,01х – 
–; г) 16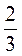Х – 0,1у – 9.
Додаткові вправи
3. Серед трьох різних чисел a, b і с число а є найменшим, а число с – найбільшим. Знайдіть знак числа b, якщо:
A) abc > 0 i ac < 0; б) abc > 0 i ac > 0; в) аbс > 0 і а + с = 0;
Г) abc < 0 i ab < 0; д) abc < 0 i c > 0; е) а + b = 0.
Узагальнення вивчення правил і властивостей множення раціональних чисел.
4. Із міста А до міста В, відстань між якими 450 км, виїхав автомобіль зі швидкістю 75 км/год. На якій відстані від міста В буде автомобіль через t год? Складіть вираз для розв’язання задачі та знайдіть його значення, якщо t = 2 год; 3,5 год.
Повторюємо задачі на рух.
5. Логічні вправи на повторення. Який рисунок пропущено?
?
V. Підсумки уроку
Тестові запитання
1) У виразі -3а – 2b коефіцієнт: а) -3; б) 2; в) -32; г) -6.
2) У виразі – abc коефіцієнт: а) а; б) – а; в) – abc; г) -1.
VI. Домашнє завдання
1. Спростіть вираз та знайдіть його коефіцієнт:
А) х – (-1,5) – 4; б) -0,8 – а – (-5) – 15; в) -2,5х – у – (0,4); г) –Х – 0,5у; д) – – 
– 25а – 14; є) 64а – 
– 
–
.
2. Спростіть вираз: а) -24-
–
; б) 0,25ас – 3 – 
.
3. Із міст А і В, відстань між якими 420 км, одночасно виїхали назустріч один одному два автомобілі. Швидкість одного з них 70 км/год, а другого – 75 км/год. Яка відстань буде між автомобілями через t год? Складіть вираз для розв’язання задачі та знайдіть його значення, якщо t = 1,5 год; 2 год.
(2 votes, average: 4,50 out of 5)