
Мета: формувати уявлення про швидкість руху тіла.
Дидактичні задачі. Вдосконалювати навички усних обчислень. Актуалізувати уміння розв’язувати прості задачі з величинами: продуктивність праці, час роботи, загальний виробіток на знаходження продуктивності праці; у дослідженні задачі змінити ситуації ( зміна величин) й одержати задачу з описом процес руху тіла, в якій шуканою є кількість кілометрів, що долає об’єкт за одиницю часу; дослідити вплив цієї зміни на розв’язання задачі; ознайомити з поняттям
Розвивальна задача: розвивати логічне мислення учнів при дослідженні залежності швидкості від зміни числового
ХІД УРОКУ
І. МОТИВАЦІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ
У світі, що довкола рухаються люди, машини, тварини… Літають літаки, птахи… Плавають кораблі, риби… У повсякденному житті ми самі рухаємось і спостерігаємо за рухом інших тіл. Хтось або щось рухається швидше чи повільніше за нас, за інших. Що означає, коли одне тіло переганяє інше чи відстає від іншого? Яка величина характеризує рух тіла? Сьогодні на уроці ми маємо зробити відкриття про це.
ІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ ТА СПОСОБІВ ДІЇ
1. Усна лічба.
Завдання №1 із робочого зошита виконується учнями самостійно.
2. Усне опитування. (Можна користуватися табличкою з робочого зошита на с. 4 № 3 та блокнотом на с. 15 підручника).
Які основні величини ви знаєте? (Довжина, маса, місткість). Назвіть групу величин, пов’язаних із масою. ( Маса 1 предмета, кількість предметів, загальна маса.) Наведіть приклад задачі з цією групою величин. Назвіть групу величин, пов’язаних із довжиною ( місткістю). Наведіть приклади задач. Які група взаємопов’язаних величин описує ситуацію купівлі-продажу? Роботи? Зіставте всі ці групи величин; що в них спільне? Назвіть величини, які характеризують величину одиниці виміру. ( Маса 1, довжина 1, місткість 1, ціна, продуктивність праці.) Назвіть величини, що характеризують загальну величину. Яким компонентом є загальна величина? (Добутком.) Величина одиниці виміру? (Першим множником.) Кількість або час (другим множником.) Як знайти значення загальної маси, довжини, місткості, вартості, загального виробітку? Наведіть приклад задачі на знаходження загальної величини. Як найти масу 1 предмета? Наведіть приклад задачі на знаходження значення величини одиниці виміру. Сашко склав таку задачу: “Машина подолала 180 км за 3 години, долаючи щогодини однакову відстань. Скільки кілометрів проїжджала машина за 1 годину?” Чи можна скласти таку задачу? Як знайти кількість або час? Наведіть приклад задачі на знаходження кількості; часу.
ІІІ. ПРОВЕДЕННЯ ДОСЛІДЖЕННЯ.
1. Ознайомлення учнів зі швидкістю руху тіла.
Завдання №1 виконується колективно.
До задачі 1) на дошці виконуємо короткий запис у вигляді таблиці, будуємо схематичний рисунок, записуємо розв’язання:

|
20
 ?
?

4
Розв’язання
20 : 4 = 20 (км) – стільки кабелю прокладали робітники за 1 годину.
Зіставляємо задачу 2 і задачу 1. Помічаємо, що в них містяться одні й ті самі числові дані та аналогічні шукані, але дещо відрізняється ситуація. В цій задачі йдеться не про роботу, а про рух хлопчика. У короткому записі попередньої задачі на дошці виконуємо зміни: продуктивність праці в попередній задачі – це довжина кабелю, що прокладали робітники за 1 годину; в задачі 2 замість продуктивності праці маємо записати “відстань, яку долає хлопчик за 1 годину або подоланий шлях за 1 год”. Час роботи треба замінити на час руху. Загальний виробіток в попередній задачі – це довжина кабелю, що проклали робітники за 4 години. В задачі 2 – це відстань, яку подолав хлопчик за 4 години – загальна відстань або краще – подоланий шлях. Зміни у схематичному рисунку не виконуються. Пояснюємо його: цілий відрізок означає, з одного боку подоланий хлопчиком шлях – 20 км, а з іншого – час його руху – 4 год. Маленький відрізок означає шлях, що долав хлопчик щогодини – він є шуканим.
З’ясовуємо, чи матимуть задачі 1 і 2 однакові розв’язання. Оскільки числові дані, шукане та зв’язки між ними та шуканим не змінилися, то, власне, розв’язання не зміниться; оскільки змінилася ситуація задачі, то треба буде виправити пояснення.
|
 20
20
 ?
?

4
Розв’язання
20 : 4 = 20 (км) долає хлопчик за 1 годину.
Повідомляємо, що шлях, який долає тіло за одиницю часу, називається швидкістю руху тіла. В цій задачі ми знайшли швидкість руху хлопчика – 20 км за 1 годину. Незручно писати розгорнено “20 км за 1 год”, тому скорочують позначення “20  ” або ” 20 км/год”, а його читають так само.
” або ” 20 км/год”, а його читають так само.
Повертаємось до розв’язання задачі, пояснюємо числа, які записані у рівності. Маємо величини: подоланий шлях, час руху, швидкість руху. Показуємо буквені позначення цих величин. З’ясовуємо, якою арифметичною дією в цій задачі знайшли швидкість руху, яким чином. Формулюємо правило знаходження швидкості руху, записуємо його за допомогою буквених позначень величин у вигляді формули двома способами: із рискою дробу як знаком ділення та за допомогою знаку ділення – двокрапки. Чому доцільно показати запис формули із рискою дробу? Для того, щоб учні могли швидко відтворити цю формулу: більшість учнів знає одиниць швидкості  , у кілометрах вимірюється подоланий шлях, а у годинах час руху; замість найменувань запишемо величину і маємо:
, у кілометрах вимірюється подоланий шлях, а у годинах час руху; замість найменувань запишемо величину і маємо: 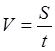 .
.
Далі обговорюємо, у яких одиницях вимірюється шлях; час. Наводимо приклади одиниць вимірювання швидкості:  .
.
Звертаємо увагу на опорний конспект у рамочці, пояснюємо, що означенням швидкості доцільно користуватися при розв’язуванні наступного завдання.
2. Первинне закріплення поняття швидкості.
Завдання №2 виконується колективно.
6 м/ год означає, що равлик щогодини долає по 6 м; 950 км/год означає, що літак щогодини долає по 950 км і т. п.
ІУ. ФОРМУВАННЯ ВМІНЬ І НАВИЧОК. ЗАКРІПЛЕННЯ ВИВЧЕНОГО
1. Закріплення поняття швидкості руху тіла.
Завдання №3 виконується учнями колективно.
Швидкість руху пішохода 5 км за годину – 5км/год; швидкість руху бджоли 7 м за секунду – 7 м/с; швидкість руху літака 15 км за хвилину – 15 км/хв; швидкість руху лижника в м за хвилину – в м/хв. Зазначимо, що одиниці швидкості на дошці доцільно записувати за допомогою риски дробу, щоб діти ще раз переконалися, що швидкість – це шлях розділений на час руху.
2. Закріплення правила знаходження швидкості.
Завдання №2 із робочого зошита виконується з коментарем.
Заповнюючи таблицю, учні спочатку відтворюють правило знаходження швидкості, а потім виконують арифметичну дію, називають і записують її результат.
3. Дослідження зміни швидкості від зміни відстані при однаковому часі.
Завдання №4 виконується колективно. Записи виконуються учнями і в зошиті, і на дошці.
Виконуємо короткий запис, записуємо формулу швидкості і розв’язання:
1) 2)
S = 20 км S=60 км
T = 4 год t = 4 год
V – ? V – ?
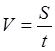
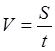
V = 20 : 4 V = 60 : 4
V = 5 км/год V= 15 км/год
Порівнюємо умови: час руху однаковий, різні значення шляху – в задачі 2) шлях збільшився. Порівнюємо значення швидкостей і з’ясовуємо, як зміна шляху вплинула на швидкість, робимо висновок.
Аналогічно працюємо над задачами 3 і 4.
4. Формування уміння розв’язувати задачі з величинами S, V, t.
Учням з високим рівнем пізнавальних потреб і можливостей можна запропонувати завдання № 3 із робочого зошита ( короткий запис задачі у вигляді таблиці).
Решта учнів у цей час виконує завдання № 2 робочого зошита. Можна запропонувати учням попрацювати в парах.
5. Розвиток логічного мислення учнів.
Маса двох ялинкових шишок і одного жолудя – 152 г. А маса двох жолудів та однієї ялинкової шишки – 94 г. Що важче: одна ялинкова шишка чи один жолудь і на скільки?
Розв’язання. На малюнку умовно позначимо жолуді квадратиками, шишки – кружками. За умовою, маса двох ялинкових шишок і одного жолудя – 152 г, а маса двох жолудів та однієї ялинкової шишки – 94 г. Покажімо це на схемі:

152 г

94 г
І спосіб. Розташуємо малюнки по-іншому:
152 г


94 г
З цього малюнка бачимо, що маса шишки більша маси жолудя. Але лишається питання: “На скільки маса шишки більша маси жолудя?”. (152 – 94) – так ми дізнаємося, на скільки маса шишки більша за масу жолудя.
ІІ спосіб. Збільшимо в першому випадку кількість шишок і жолудів у 2 рази: 4 шишки та 2 жолуді, тоді б їх маса була 152 * 2 = 304 г. Маємо:
304 г


94 г
304 – 94 = 210 (г) маса 3 шишок; 210 : 3 = 70 (г) маса 1 шишки.
Але можна було збільшити в 2 рази кількість шишок і жолудів в другому випадку. Маємо: 2 шишки та 4 жолуді; їх маса 94 * 2 = 188 (г)
152 г


188 г
188 – 152 = 36 (г) маса 3 жолудів; 36 : 3 = 12 ( г) маса 1 жолудя.
Тепер відповімо на запитання задачі: 70 – 12 = 58 (г) на стільки маса шишки більша за масу жолудя.
УІІ. ПОЯСНЕННЯ ЗАВДАННЯ ДЛЯ ДОМАШНЬОЇ РОБОТИ
Завдання № 5 – виконати обчислення із застосуванням письмового прийому; за бажанням перевірити результати. Завдання №6 – пригадати правило знаходження швидкості та формулу швидкості та розв’язати задачу. Учні з високим рівнем пізнавальних потреб можуть скласти і розв’язати хоча б одну обернену задачу.
УІІІ. ПІДСУМОК. РЕФЛЕКСІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ
Яка група взаємопов’язаних величини описує рух тіла? Як ви розумієте швидкість? Чому дорівнює швидкість хлопчика, якщо він за годину долає по 5 км? Що означає швидкість машини 58 км/год? Якими буквами позначаються швидкість, подоланий шлях та час руху відповідно? Як знайти швидкість руху тіла, якщо знаємо подоланий шлях та час руху? Запишіть формулу швидкості. Як нею користуватися для розв’язування задач? Треба у формулу замість подоланого шляху підставити його значення, а замість часу руху – його значення та виконати обчислення.
