Урок № 14
Тема. Спільний знаменник кількох дробів. Зведення звичайних дробів до найменшого спільного знаменника
Мета: на основі основної властивості дробу сформувати уявлення учнів про зміст поняття зведення дробів до спільного знаменника, а також розпочати роботу з вироблення вмінь зводити дроби до найменшого спільного знаменника.
Тип уроку: засвоєння нових знань.
Хід уроку
І. Перевірка домашнього завдання
Оскільки попередня тема опрацьована, то фронтальної перевірки домашнього завдання (задля економії
ІІ. Актуалізація опорних знань
Усні вправи
1. Обчисліть: |
|
|
2. Знайдіть серед чисел рівні й поясніть: 
; 
; 1; 
; 
; 
; 
; 
; 0,5; 
; 0,4.
3. Знайдіть НСК чисел (найраціональнішим способом): а) 4 і 8; б) 12 і 16; в) 12 і
4. Чи існує таке натуральне число, яке в добутку із числом 6 дало б число: а) 18; б) 27; в) 3? Відповідь обгрунтуйте.
ІІІ. Формування знань
@ На уроці треба розглянути два питання.
1. Що означає “звести дріб до нового знаменника”?
2. Як звести два (і більше дробів) до найменшого спільного знаменника?
Тому й викладення матеріалу можна проводити традиційно, спочатку розглянувши приклад на зведення дробу до нового знаменника, а потім алгоритм зведення дробів до найменшого спільного знаменника.
Результатом такої роботи може бути конспект № 9.
Конспект 9 | |
Зведення дробів до НСЗ | |
1. Зведення одного дробу до нового знаменника:
1) с : b = n – додатковий множник; 2) 2. Зведення кількох дробів до НСЗ (найменший спільний знаменник): 1) знайти НСК знаменників > НСЗ; 2) поділити НСЗ на кожний знаменник > додатковий множник; 3) чисельник і знаменник дробу помножити на додатковий множник | Приклад
Оскільки 96 : 4 = 24, то Приклад Звести Оскільки НСК (5; 7) = 35, то НСЗ = 35. 35 : 5 = 7; 35 : 7 = 5,тому
|
треба звести до знаменника с.
.
.
і 
до НСЗ.
; 
IV. Формування вмінь
@ Відповідно до схеми пояснення матеріалу, розв’язуємо спочатку вправи на:
А) формування вмінь зводити дріб до нового знаменника;
Б) формування вмінь використовувати алгоритм зведення кількох дробів до НСЗ.
Розв’язування вправ
І рівень
Усні вправи
Назвіть дріб зі знаменником 16, який дорівнює дробу: ; 
; 
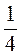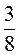. (Для кращого сприйняття можна умову записати у вигляді рівності: 
)
Знайдіть НСК знаменників дробів: a) 
і 
; б) 
і 
; в) 
і 
.
Краще спочатку просто знайти НСЗ для даних дробів.
ІІ, III рівні
Письмові вправи
1. Зведіть до знаменника 48 дроби: ; ; ; 
; 
; 
.
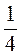2. Зведіть до найменшого спільного знаменника дроби: а) 
і 
; б) 
і 
; в) і 
; г) 
і 
.
3. Зведіть до найменшого спільного знаменника дроби: а)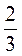 
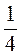, і ; б) 
, і 
; в) 
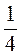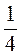, і 
.
Додатково доцільно розв’язати задачі на повторення алгоритмів порівняння звичайних дробів з однаковими знаменниками; їх додавання і віднімання, а також матеріалу, пов’язаного із мішаними числами.
Задача1. При яких значеннях а нерівність правильна?
А) 
; б) 
; в) 
; г) 
.
Задача 2. Домогосподарка приготувала 13 кг вишневого варення і 15 кг полуничного. Вишневе вона розлила порівну в 15 банок, а полуничне – у 17 банок. Скільки кілограмів варення кожного виду було в одній банці?
Задача 3. Знайдіть пропущені букви
Задача 4. Знайдіть пропущені рисунки:
V. Підсумки уроку
Повторити засвоєні терміни і поняття можна під час виконання так званого “німого диктанту”:
@Вчитель заздалегідь за дошкою готує записи, що містять перетворення, розглянуті на уроці, і просто показує об’єкти, назву якого учні повинні були засвоїти. Наприклад:
VI. Домашнє завдання
1. Зведіть до знаменника 36 дроби: ; ; 
; ; 
; 
.
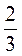2. Зведіть до найменшого спільного знаменника дроби: а) 
і 
; б) і 
; в) і ; г) 
і 
.
3. Зведіть до найменшого спільного знаменника дроби: а) , 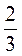і ; б) , і 
; в) 
, 
і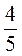 
.
4. Запишіть неправильним дробом: 
, 
, 
.
5. Виконайте дії: а) 
; б) 
; в) 
; г) 
.
(1 votes, average: 5,00 out of 5)